正三角形ＡＢＣと長さが１㎝の棒ＰＱがあります。最初、点Ｐは辺ＡＢ上に、点Ｑは辺ＢＣ上にあり、ＰＢの長さとＱＢの長さはともに１㎝です。線ＰＱを次のように正三角形の内側で動かします。図１のように、線ＰＱを、初めに点Ｑを中心として点Ｐが正三角形の辺上に来るまで回転させます。次に、点Ｐを中心として点Ｑが正三角形の辺上に来るまで回転させます。このように、点Ｑと点Ｐを交互に中心とする線ＰＱの回転を、点Ｐが最初の位置に来るまで繰り返します。
※ 画像はすべて、クリックすると拡大します。
正三角形ＡＢＣの１辺の長さが次の各場合のとき、点Ｐがえがく線の長さは、半径１㎝の円の周の長さの何倍ですか。
(１) ３㎝
(２) ４㎝
(３) １２３４㎝
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
長さ１㎝の棒ＰＱが１辺３㎝の正三角形の内部を回転しながら移動する様子を、点Ｐが回転したときだけ図に表すと次のようになります。
この図のように、点Ｑを中心として３回目に回転移動したとき、点Ｐは辺ＡＢ上のスタート地点へ戻ります。
※ 画像はすべて、クリックすると拡大します。
上の図の青い孤はどれも中心角が１２０度なので、それを３本集めると中心角の合計は１２０×３＝３６０度になります。
つまり、点Ｐが動いた長さはちょうど半径１㎝の円周１個分と等しいので、答えは１÷１＝１倍になります。
(２)
１辺４㎝の正三角形ＡＢＣの辺ＡＢ上にある赤い点から、次の図のように棒ＰＱが回転しながら移動するとき、点Ｐが動いた線は、
・辺ＢＣ上→中心角１２０度のおうぎ形が２個できる
・辺ＣＡ上→半円が１個できる
となります。
その後、辺ＡＢ上を進むときは次の図のように点Ｐが赤いスタート地点を飛び越えてしまうので、
・辺ＡＢ上→中心角１２０度のおうぎ形が２個できる
・辺ＢＣ上→半円が１個できる
という流れで２周目に突入します。
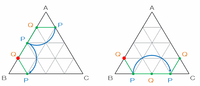
２周目に突入した棒ＰＱは、次の図のように
・辺ＣＡ上→中心角１２０度のおうぎ形が２個できる
・辺ＡＢ上→半円が１個できる
という流れで回転移動したとき、点Ｐが赤いスタート地点に到着します。
つまり、点Ｐが動いてできた線は
・中心角１２０度のおうぎ形の孤が２×３＝６個
・半円が３個
なので、中心角の合計は１２０×６＋１８０×３＝１２６０度になります。
したがって、答えは１２６０÷３６０＝３.５倍です。
(３)
１辺１２３４㎝の正三角形ＡＢＣの辺ＡＢ上にある赤い点から、次の図のように棒ＰＱが回転しながら辺ＢＣ上を移動するとき、点Ｐが動いた線は、
・中心角１２０度のおうぎ形が左右のはしに１個ずつできる
・半円が(１２３４－２×２)÷２＝６１５個できる
となり、次の辺ＣＡ上は点Ｐから始まります。
また、次の図のように辺ＣＡ上を進むときには、(１２３４－１×２)÷２＝６１６個の半円ができ、次の辺ＡＢ上は点Ｑから始まります。
※ つまり、正三角形の辺を進むごとに「中心角１２０度のおうぎ形２個＋半円６１５個」と「半円６１６個」の繰り返し。
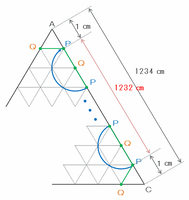
棒ＰＱが次の図のように辺ＡＢ上を進むときには、また「中心角１２０度のおうぎ形２個＋半円６１５個」ができるのですが、点Ｐは赤いスタート地点を飛び越えてしまうため、２周目突入が確定します。
また、最初は赤いスタート地点に点Ｐがいて、１周したらそこには点Ｑが来たので、もう１周したら赤い地点に点Ｐが来ることも分かります。
これまでに分かったことをもとにして、棒ＰＱが正三角形の内部を２周するときに点Ｐが動いてできる線についてまとめてみると、
【１周目】
・辺ＢＣ上→中心角１２０度のおうぎ形２個＋半円６１５個
・辺ＣＡ上→半円６１６個
・辺ＡＢ上→中心角１２０度のおうぎ形２個＋半円６１５個
【２周目】
・辺ＢＣ上→半円６１６個
・辺ＣＡ上→中心角１２０度のおうぎ形２個＋半円６１５個
・辺ＡＢ上→半円６１６個
となるので、中心角１２０度のおうぎ形は全部で２×３＝６個、そして半円は(６１５＋６１６)×３＝３６９３個できます。
１２０×６＝７２０度なので、中心角１２０度のおうぎ形を６個つなげると円が７２０÷３６０＝２個できます。
また、半円３６９３個を全部つなげると円が３６９３÷２＝１８４６.５個できるので、答えは２＋１８４６.５＝１８４８.５倍になります。
【追記】
(１)で１辺３㎝、(２)で１辺４㎝の場合を解いた時点で「あー、１辺の長さが奇数なら１周、偶数なら２周する仕組みかも・・・」と気がつけば話は早いんだけど、もしそんなふうに勘が働かなくても普通に解けますね。
PR
