１辺が１２㎝の正方形ＡＢＣＤがあります。点Ｐは点Ａからスタートして、毎秒３㎝の速さで反時計回りに辺の上を動きます。点Ｑは同時に点Ｃからスタートして、毎秒２㎝の速さで同じように反時計回りに辺の上を動きます。次の問いに答えなさい。
※ 画像はクリックする拡大します。
(１)
スタートしてから２秒後、４つの点Ａ、Ｐ、Ｃ、Ｑを順に結んでできる図形の面積を求めなさい。
(２)
スタートしてから５秒後、４つの点Ａ、Ｐ、Ｃ、Ｑを順に結んでできる図形の面積を求めなさい。
(３)
スタートしてから４秒後から８秒後までの間で、４つの点Ａ、Ｂ、Ｐ、Ｑを順に結んでできる図形が長方形になるのは何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
スタートから２秒後、点Ｐは頂点Ａから右へ３×２＝６㎝、点Ｑは頂点Ｃから左へ２×２＝４㎝進んでいます。
そのとき、四角形ＡＰＣＱは次の図のような台形になっているので、面積は(４＋６)×１２÷２＝６０㎠になります。
※ 画像はすべて、クリックすると拡大します。
(２)
スタートから５秒後、点Ｐは頂点Ａから３×５＝１５㎝進んだので、頂点Ｂから真上へ１５－１２＝３㎝離れた地点にいます。
点Ｑは頂点Ｃから左へ２×５＝１０㎝進んだので、頂点Ｄまで残り１２－１０＝２㎝の地点にいます。
そのときの四角形ＡＰＣＱを図に表してみると次のようになります。
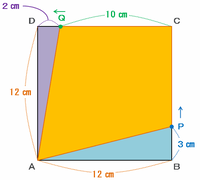
上の図の頂点ＡからＣへ補助線を引いて、ＡＰＣＱを２つの三角形に分けて面積を求めてもＯＫなのですが、今回は「全体からいらない部分の面積を引く」という方法で答えを求めてみます。
※ 「全体」と「いらない部分」を見分ける技術は、図形問題を解くときに欠かせないものだから。
まずは上の図の各部分の面積をそれぞれ求めてみると・・・
・正方形ＡＢＣＤの面積→１２×１２＝１４４㎠
・三角形ＰＡＢの面積→１２×３÷２＝１８㎠
・三角形ＤＡＱの面積→１２×２÷２＝１２㎠
となるので、求める四角形ＡＰＣＱの面積は１４４－(１８＋１２)＝１１４㎠になります。
(３)
４秒後から８秒後までの間で長方形になるときを見つければＯＫなので、まずは点ＰとＱをそれぞれ４秒間進めてみます。
スタートから４秒後、点Ｐは頂点Ａから３×４＝１２㎝進んだので、ちょうど頂点Ｂの真上にいます。
点Ｑは頂点Ｃから左へ２×４＝８㎝進んだので、頂点Ｄまで残り１２－８＝４㎝の地点にいます。
そのときのＡＢＰＱを図に表してみると、次のような三角形になっています。
長方形にするためには、少なくとも向かい合わせの辺を平行にしなければならないので、とりあえず点Ｑを頂点Ｄまで進めて、辺ＡＱと辺ＢＰが平行になるようにします。
このとき、点Ｑが頂点Ｄまでの残り４㎝を進むには４÷２＝２秒かかるので、その間に点Ｐは頂点Ｂから真上へ３×２＝６㎝の地点まで進みます。
したがって、スタートから４＋２＝６秒後の四角形ＡＢＰＱは、次の図のような台形になっています。
つまり、スタートから６秒後の点ＰとＱは垂直方向へ１２－６＝６㎝離れているので、その差がゼロになったとき、次の図のように四角形ＡＢＰＱは長方形になります。
上の図の点ＰとＱは向かい合わせに進んでいるので、２つの点の距離の差がゼロになるまでにかかる時間は６÷(３＋２)＝１.２秒です(旅人算)。
つまり、四角形ＡＢＰＱが長方形になるのは６秒後の図からさらに１.２秒たったときなので、答えは６＋１.２＝７.２秒後になります。
PR
