中心が同じ点Ｏである２つの円があります。大きい円の半径は２㎝、小さい円の半径は１㎝で、円の中心からのびている直線と大きい円との交わった点をＡ、小さい円との交わった点をＢとします。点ＰとＱは大きい円の周の上を、Ｐは反時計回りに１０秒で１周し、Ｑは時計回りに５秒で１周します。また、点Ｒは小さい円の周の上を反時計回りに１０秒で１周します。最初、２つの点Ｐ、Ｑは点Ａにあり、点Ｒは点Ｂにあります。３つの点Ｐ、Ｑ、Ｒが同時に動き始めるとき、次の各問いに答えなさい。ただし、３つの点Ｐ、Ｑ、Ｒはそれぞれ一定の速さで動くものとします。
※ 画像はクリックすると拡大します。
(１)
３つの点Ｐ、Ｑ、Ｒが初めてひとつの直線の上に並ぶのは、動き始めてから何秒後ですか。
(２)
３つの点Ｐ、Ｑ、Ｒを結んでできる三角形の面積を考えます。
①
三角形ＰＱＲの面積が最も大きくなるとき、その面積は何㎠ですか。
②
三角形ＰＱＲの面積が２回目に最も大きくなるのは動き始めてから何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは３つの点が１秒間に進む角度と動く方向をそれぞれ確認してみると、
・点Ｐ→１秒間に３６０÷１０＝３６度ずつ、反時計回りに進む
・点Ｑ→１秒間に３６０÷５＝７２度ずつ、時計回りに進む
・点Ｒ→１秒間に３６０÷１０＝３６度ずつ、反時計回りに進む
となるので、点ＰとＲは進む速さも方向も同じであり、円の中心Ｏと点Ｐ、Ｒの３つを結ぶと常に一直線となることが分かります。
また、「点Ｐ、Ｒ」と「点Ｑ」が進む速さは３６度：７２度＝１：２なので、次の図のように３つの点Ｐ、Ｑ、Ｒが初めてひとつの直線の上に並んだとき、
・点ＰとＲが進んだ角度→１８０×３分の１＝６０度
・点Ｑが進んだ角度→１８０×３分の２＝１２０度
となることが分かります(１８０度を１：２に比例配分)。
※ 画像はすべて、クリックすると拡大します。
点ＰとＲは１秒間に３６度の割合で進むので、６０度進むのはスタートしてから６０÷３６＝３分の５秒後になります。
【補足】
「毎秒３６度ずつ進む点と７２度ずつ進む点が、逆方向へ動いて合わせて１８０度進むまでにかかる時間」という感じで、旅人算っぽく１８０÷(３６＋７２)＝３分の５秒後と求めてももちろんＯＫです。
(２)の①
まずはこの問題を解くのに必要な予備知識の確認から始めます。ものすごく基本的な話なので「そこまで馬鹿にすんな！」と思う人もいるかもしれませんが、そういう場合は広い心でスルーしてください。
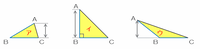
次の図の三角形ア～ウは、どれも辺ＡＢとＢＣの長さが等しい二等辺三角形です。
この３つの三角形の底辺をすべてＢＣとすると、高さがもっとも高くなるのは角ＡＢＣが直角となるイのときなので、ア～ウの中で面積が最大なのはイであることが分かります。
つまり、辺ＡＢとＢＣの長さが等しい二等辺三角形の面積が最大となるのは、角ＡＢＣが直角となるときであり、そのときのＡＢＣは直角二等辺三角形になります。
次の図の三角形ＯＰＱは辺ＯＰとＯＱの長さがどちらも２㎝で等しいので、その２辺が作る角ＰＯＱが直角となるとき、三角形ＯＰＱの面積は最大となります。
また、そのときのＯＰＱは直角二等辺三角形なので、面積は２×２÷２＝２㎠です。
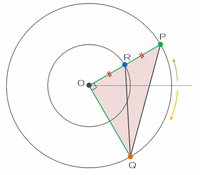
上の図の辺ＯＲとＲＰの長さはどちらも常に１㎝で等しいので、三角形ＰＱＲの面積はいつでもＯＰＱの半分になります。
※ 三角形ＰＯＱの面積は常に辺ＲＱで２等分されるから。
つまり、三角形ＯＰＱの面積が最大であればＰＱＲの面積も最大となるので、三角形ＰＱＲの面積の最大値は、上の図の三角形ＯＰＱの面積の半分にあたる２÷２＝１㎠です。
(２)の②
さっきの図だと、「点Ｐ、Ｒ」と「点Ｑ」の動いた角度の合計が９０度になったときに三角形ＰＯＱの内角である角ＰＯＱが直角となり、そのとき円の中心角の残りは３６０－９０＝２７０度でした。
逆にいえば、「点Ｐ、Ｒ」と「点Ｑ」の動いた角度の合計が２７０度になったとき、残りの角度は直角となるので、三角形ＯＰＱは再び直角二等辺三角形になります。
また、「点Ｐ、Ｒ」と「点Ｑ」が進む速さは１：２なので、動いた角度の合計が２７０度となったとき、
・点ＰとＲが進んだ角度→２７０×３分の１＝９０度
・点Ｑが進んだ角度→２７０×３分の２＝１８０度
となることが分かります(次の図参照)。
上の図で「点Ｐ、Ｒ」の動いた角度が９０度となるのは、スタートしてから９０÷３６＝２.５秒後です。
PR
