次のグラフは、きよし君が途中で休憩をとりながらＡ地点から５㎞離れたＢ地点まで歩いていく様子を表しています。ともひさ君はきよし君より４０分遅れてＡ地点を自転車で出発し、同じ道をＢ地点に向かい５分走ったときに転んだので、５分間休憩し、再びＢ地点に向かい出発し、転ぶ前と同じ速さで進み、ともひさ君が出発してから１５分後にきよし君を追い越して先にＢ地点に到着しました。このとき、次の各問いに答えなさい。
※ 画像はクリックすると拡大します。
(１)
ともひさ君の進行する様子を定規を用いてグラフに書き入れなさい。ただし、グラフを描いたときに用いた補助線はそのまま残しておきなさい。また、方眼の目盛りは利用してよいが、それ以外の目盛りはとってはならないものとします。
(２)
ともひさ君の速さを求めなさい。
(３)
ともひさ君が転ばなかったら、ともひさ君が出発してから何分できよし君に追いつくか求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
Ａ地点を出発したともひさ君がきよし君に追いつくまでの１５分間は、
・自転車で転ぶ前の５分間
・転んで休憩中の５分間
・再スタート後の５分間
の３つの部分に分けられます。
つまり、ともひさ君の実際の走行時間は１５－５＝１０分間なので、次のグラフのようにきよし君より４０＋５＝４５分遅れてＡ地点をスタートすれば、１０分後にはきよし君に追いつきます。
※ 画像はすべて、クリックすると拡大します。
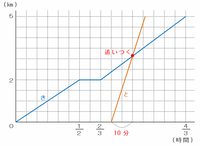
ただし、実際には再スタート後の走行時間は５分なので、次のグラフのようにきよし君に追いついた時刻から５分さかのぼり、そこから線を左へまっすぐ伸ばして５分間の休憩を表します。
また、ともひさ君はきよし君より４０分＝３分の２時間遅れてＡ地点を出発したので、下のグラフのように「０㎞・３分の２時間」と「５分間の休憩の左端」を直線で結べば、ともひさ君が進行する様子が完成します。
なお、下のグラフの緑色の直線と最初のオレンジ色の直線は速度が同じなので平行になっているはずです。
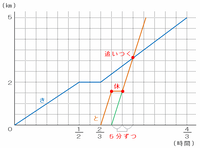
(２)
休憩後のきよし君は５－２＝３㎞を３分の４－３分の２＝３分の２時間で進んだので、そのときの速さは３÷３分の２＝時速４.５㎞になります。
※ きよし君の休憩前の速さは２÷２分の１＝時速４㎞。休憩の前後で速さが違うので注意。
また、きよし君はともひさ君に追いつかれるまでに１５分＝４分の１時間進んだので、きよし君はその１５分間で４.５×４分の１＝１.１２５㎞進みました。
つまり次のグラフのように、ともひさ君がきよし君に追いついたのはＡ地点から２＋１.１２５＝３.１２５㎞離れた場所であることが分かります。
ともひさ君は、Ａ地点からきよし君に追いついた地点までの３.１２５㎞をノンストップなら１０分＝６分の１時間で行けるので、ともひさ君の速さは３.１２５÷６分の１＝時速１８.７５㎞です。
(３)
次のグラフのように、きよし君が休憩を終えたとき、２人の距離は２㎞離れていて、その後はきよし君が時速４.５㎞、そしてともひさ君は時速１８.７５㎞で同じ方向へ進みます。
旅人算の公式を使って、ともひさ君がきよし君に追いつくまでにかかる時間を求めてみると、２÷(１８.７５－４.５)＝５７分の８時間後になります。
ただし、答えの単位は「分」なので６０倍して単位を直すと、５７分の８×６０＝１９分の１６０分後になります。
PR
