次の図は、点Ｏを中心とする半径６㎝の円で、直径ＡＢとＣＤは直角に交わっています。点ＰはＡを出発して毎秒３㎝の速さで、ＡとＯの間を休みなく往復します。点ＱはＢを出発して毎秒２㎝の速さで、ＢとＯの間を休みなく往復します。またＰとＱは同時に出発します。
※ 画像はすべて、クリックすると拡大します。
(１)
ＰとＱが出発してから５秒後の三角形ＣＰＱの面積は( ア )㎠です。また、次に同じ面積になるのは出発してから( イ )秒後です。
(２)
ＰとＱが出発してから１１６秒後の三角形ＣＰＱの面積は( )㎠です。
(３)
円から三角形ＣＰＱを除いた部分の面積が１０７.０４㎠となるときがあります。６回目にこの面積となるのはＰとＱが出発してから( )秒後です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
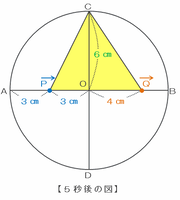
まずはスタートから５秒後の点ＰとＱの位置を確認しておくと、それぞれ次のようになります。
・Ｐ→３×５＝１５㎝進む。１５÷６＝２余り３なので、ＡＯ間を１往復した後、Ａから右へ３㎝進んだ。
・Ｑ→２×５＝１０㎝進む。１０－６＝４㎝なので、ＯからＢへ向けて４㎝進んだ。
そのときの三角形ＣＰＱは、次の図のように底辺が３＋４＝７㎝、高さは６㎝になるので、面積は７×６÷２＝２１㎠になります。
また、毎秒３㎝で進む点ＰがＰＯ間の３㎝を往復するのにかかる時間は３×２÷３＝２秒、そして毎秒２㎝で進む点ＱがＱＢ間の２㎝を往復するのにかかる時間も２×２÷２＝２秒なので、スタートから５＋２＝７秒後には、次の図のように点ＰとＱがどちらも５秒後のときとまったく同じ位置に来ています。
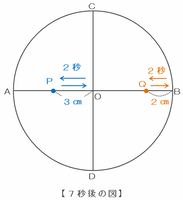
以上から、アには２１が、そしてイには７があてはまります。
(２)
まずはスタートから１１６秒後の点ＰとＱの位置を確認しておくと、それぞれ次のようになります。
・Ｐ→３×１１６＝３４８㎝進む。３４８÷６＝５８なので、ＡＯ間をちょうど５８÷２＝２９往復してＡに着いた。
・Ｑ→２×１１６＝２３２㎝進む。２３２÷６＝３８余り４なので、ＢＯ間を３８÷２＝１９往復してＢに着いた後、さらにＯへ向けて４㎝進んだ。
つまり、そのときの三角形ＣＰＱは次のように、底辺が６＋２＝８㎝、高さが６㎝になるので、面積は８×６÷２＝２４㎠になります。
(３)
点Ｐは１２÷３＝４秒おきにＡへ戻り、点Ｑは１２÷２＝６秒ごとにＢへ戻るので、４と６の最小公倍数である１２秒間の中で条件にあてはまるときが何回あるのかをまずは調べてみます。
円の面積は６×６×３.１４＝１１３.０４㎠なので、問題文の条件に合うのは、三角形ＣＰＱの面積が１１３.０４－１０７.０４＝６㎠のときです。
三角形ＣＰＱの底辺を□㎝とおくと、面積が６㎠のときは□×６÷２＝６㎠という式がおけるので、底辺は６×２÷６＝２㎝となります。
スタートのとき、三角形ＣＰＱの底辺(つまりＡＢの長さ)は６×２＝１２㎝で、それが１秒ごとに３＋２＝５㎝ずつ縮まっていくので、底辺が初めて２㎝になるのはスタートから(１２－２)÷５＝２秒後です。
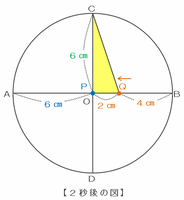
この後、点ＰとＱはそれぞれ６×２＝１２㎝進むごとに上の図の位置へと戻ってきます。
スタートから１２秒間のうち、点Ｐが上の図のようにＯの位置へ来るのは６÷３＝２秒後、６×３÷３＝６秒後、６×５÷３＝１０秒後の３回です。
※ Ａを出発した点Ｐが、ＡＯ間を片道１本、３本、５本分進んだとき。
また、１２秒間で点Ｑが上の図の位置にくるのは、４÷２＝２秒後、８÷２＝４秒後、１６÷２＝８秒後、２０÷２＝１０秒後の４回です。
つまり、スタートから１２秒間の中で点ＰとＱがどちらも上の図と同じ位置にくるのは、２秒後と１０秒後の２回であることが分かります。
次の図のように、スタートから６回目は１２秒ずつ区切ったグループの３つ目にある「１０秒」のところなので、答えは１２×２＋１０＝３４秒後になります。
PR
