図１のように、同じ形の直角二等辺三角形が２つあります。右下の三角形が、３秒間に２㎝ずつ一定の速さで矢印の方向に移動します。途中で図２のようになり、図３の位置で止まりました。
※ 画像はクリックすると拡大します。
(１) 三角形が止まるのは、移動を始めてから何秒後ですか。
(２) 図２でアとウの面積が等しくなるのは、移動を始めてから何秒後ですか。
(３) 図２でアとイの面積が等しくなるとき、緑色の線で囲まれた図形の面積は何㎠ですか。
(４) 図２で緑色の線の長さが１０２㎝になるのは、移動を始めてから何秒後ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のオレンジ色の三角形がスタート地点からゴールの位置まで進むためには、真上へ向けて２４㎝進む必要があります。
※ 画像はすべて、クリックすると拡大します。
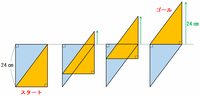
オレンジ色の三角形は３秒間で２㎝ずつ進むので、２４㎝進むのにかかる時間を□秒とおくと、３秒：２㎝＝□秒：２４㎝という比例式ができます。
したがって、オレンジ色の三角形が止まるまでにかかる時間は、３×２４÷２＝３６秒になります。
(２)
アとウの面積を等しくするためには、次の図のように三角形ＡＢＣをスタートの位置から真上へ２４÷２＝１２㎝動かして、アとウを合同にすればＯＫです。
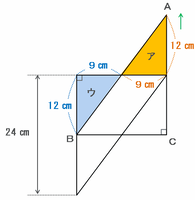
さっきの問題で三角形ＡＢＣが２４㎝進むのに３６秒かかることが分かったので、上の図の三角形ＡＢＣが１２㎝進むのはスタートしてから３６÷２＝１８秒後になります。
(３)
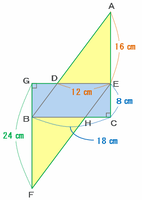
次の図の三角形アの面積を求める式は「ＤＥ×ＡＥ÷２」、そして平行四辺形イの面積を求める式は「ＤＥ×ＥＣ」と表すことができます。
アの面積を求める式には「÷２」があるので、２つの式の答えを同じにするためには、下の図のようにＡＥの長さをＥＣの２倍にする必要があります。
※ アの面積→ＤＥ×②÷２＝ＤＥ×① イの面積→ＤＥ×①
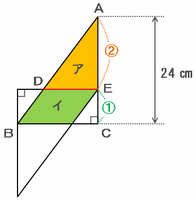
上の図のＡＥとＥＣの長さは、それぞれ比例配分を利用して次のように求められます。
・ＡＥの長さ→２４×(３分の２)＝１６㎝
・ＥＣの長さ→２４×(３分の１)＝８㎝
このとき、下の図の三角形ＡＢＣと三角形ＡＤＥは相似なので、どちらの三角形も底辺と高さの比は１８㎝：２４㎝＝３：４になっています。
つまり辺ＤＥの長さを□㎝とおくと、３：４＝□㎝：１６㎝という比例式ができるので、辺ＤＥの長さは３×１６÷４＝１２㎝になります。
これまでに分かった長さを利用して下の図全体の面積を求めてみると・・・
・三角形ＡＤＥ→底辺１２㎝で高さ１６㎝なので、１２×１６÷２＝９６㎠
・長方形ＧＢＣＥ→たて８㎝で横１８㎝なので、８×１８＝１４４㎠
・三角形ＦＨＢ→三角形ＡＤＥと同じく９６㎠
となるので、緑色の線に囲まれた図形の面積は９６×２＋１４４＝３３６㎠になります。
(４)
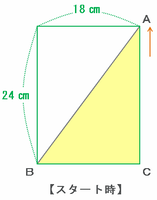
三角形ＡＢＣが真上へ向けて出発するとき、次の図の緑色の線の長さ(つまり長方形の周囲の長さ)は、(２４＋１８)×２＝８４㎝になっています。
この後、三角形ＡＢＣは真上へ向けて３秒間に２㎝の割合で進んでいきます。
三角形ＡＢＣが真上へ向けてスタートしてから３秒後、図形全体を囲む緑色の線は次の図のようになっています。
下の図はさっきの長方形のときに比べて、
・横の長さは赤い線の分だけ短くなった。
・短い斜めの線(辺ＡＤと辺ＦＧ)が増えた。
のですが、この図だけでは赤い線や斜めの線が何㎝なのか分からないので、相似を利用してそれぞれの長さを求めてみます。
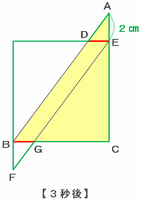
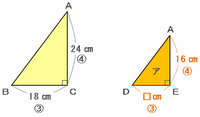
次の図の三角形ＡＢＣは、辺の長さの比が短い順に１８㎝：２４㎝：３０㎝＝３：４：５になっています。
下の２つの三角形は相似なので、三角形ＡＤＥも辺の長さの比が短い順に３：４：５になっているはずです。
上の図の三角形ＡＤＥを見てみると、辺ＡＥの長さである２㎝が比の④にあたるので、比の①は２÷④＝０.５㎝になります。
このとき、辺ＤＥの長さは比の③なので０.５×③＝１.５㎝、そして辺ＡＤの長さは比の⑤なので０.５×⑤＝２.５㎝だと分かります。
つまり次の図のように、スタートしてから３秒後の図形全体の周りの長さは、長方形だったときに比べて、
・辺ＡＤと辺ＦＧが加わるので、２.５×２＝５㎝増える。
・辺ＤＥと辺ＢＧがなくなるので、１.５×２＝３㎝減る。
ので、結局は周りの長さが５－３＝２㎝増えることになります。
スタートのときの長方形の周りの長さは８４㎝なので、それを１０２㎝にするためには１０２－８４＝１８㎝増やせばＯＫです。
三角形ＡＢＣが真上へ動くにつれて、周りの長さは３秒ごとに２㎝ずつ増えていきます。
周りの長さが１８㎝増えるのにかかる時間を□秒とおくと、３秒：２㎝＝□秒：１８㎝という比例式ができます。
したがって、答えは３×１８÷２＝２７秒後になります。
PR
