一辺が２０㎝の正方形の紙を次の図１のように折り、ＡＣを１：４に分ける点とＢＣのまん中の点を結んだ線で切り、オレンジ色の部分を取り除きます。このとき、残った紙を広げると、形は( １ )で、面積は( ２ )㎠です。( １ )は図２より選び、記号で答えなさい。
※ 画像はすべて、クリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
紙を３回折り曲げてから左側を切り取ったので、その紙を３回広げて元通りに戻してみます。
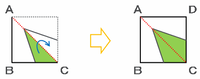
【紙を広げる その１】
１回目は次の図の赤い点線に沿って、紙を右斜め上へ広げます。
そのとき、三角形ＡＢＤと三角形ＡＤＣは線対称になっているので、赤い線の右側にも緑色の三角形ができます。
※ 画像はすべて、クリックすると拡大します。
【紙を広げる その２】
２回目は次の図の赤い点線に沿って、紙を右横へ広げます。
この場合も赤い点線の左右は線対称になるので、左側にある緑色の四角形が右側にもできます。
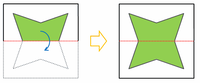
【紙を広げる その３】
最後は次の図の赤い点線に沿って、紙を下へ広げます。
このときにできた緑色の手裏剣みたいな形にもっとも近い選択肢はアになります。
(２)
紙を１回目に折り曲げたときにたての長さが半分に、そして２回目に折り曲げたときには横の長さが半分になったので、下の図の三角形ＡＢＣの底辺と高さはどちらも２０÷２＝１０㎝になっています。
つまり三角形ＡＢＣの面積は１０×１０÷２＝５０㎠になるのですが、ここからは下の図の緑色の三角形がそのどれだけにあたるのかを求めていきます。
【その１ 三角形ＥＢＣの面積を求める】
下の図のオレンジ色の三角形ＡＢＥと青い三角形ＥＢＣは、辺ＡＥと辺ＥＣの長さの比が１：４になっています。
その２つの辺を底辺とすると、２つの三角形は高さが等しくなるので、面積比も底辺の長さの比と同じく１：４になります。
三角形ＡＢＣの面積は５０㎠なので、下の図の青い三角形ＥＢＣの面積は５０×(５分の４)＝４０㎠になります(比例配分)。
【その２ 三角形ＥＤＣの面積を求める】
下の図の点Ｄは辺ＢＣの真ん中にあるので、辺ＢＤと辺ＤＣの長さの比は１：１です。
また、青い三角形ＥＢＤと緑色の三角形ＥＤＣは高さが等しいので、面積比は底辺の比と同じく１：１になっています。
つまり、緑色の三角形ＥＤＣの面積は三角形ＥＢＣの半分にあたるので、その面積は４０÷２＝２０㎠になります。
下の図のように、紙を広げた図形には緑色の三角形が全部で８個できるので、面積の合計は２０×８＝１６０㎠になります。
PR
