あるお菓子屋さんでは、Ａ、Ｂのお菓子を毎日合計９００個作ります。１５個入りの箱にはＡ１０個とＢ５個を、９個入りの箱にはＡ３個とＢ６個を、８個入りの箱にはＡ４個とＢ４個を入れます。
(１)
ある日、ＡとＢを１１：７の割合で作って、１５個入りと８個入りの箱に入れたら、Ａが３０個余りました。この日は、１５個入りの箱が( )箱、８個入りの箱が( )箱できました。
(２)
次の日は、ＡとＢを７：８の割合で作って、１５個入りと９個入りの箱に入れたら、すべてぴったり入りました。この日は、１５個入りの箱が( )箱、９個入りの箱が( )箱できました。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずはお菓子ＡとＢの合計である９００個を１１：７の割合に比例配分すると、
・お菓子Ａ→９００×１８分の１１＝５５０個
・お菓子Ｂ→９００×１８分の７＝３５０個
となります。
ただし、２種類の箱にお菓子を詰め終わったとき、Ａは３０個余ったので、実際に箱へ詰めたお菓子Ａの数は５５０－３０＝５２０個、そしてお菓子Ｂの数は３５０個です。
つまり、最初の時点でお菓子ＡはＢよりも５２０－３５０＝１７０個多いのですが、もし８個入りの箱だけを使うと、ＡとＢを同じ数ずつ詰めるので差が縮まりません。
そこで次の図のように、
・まずは１５個入りの箱(図のアとイ)にお菓子を詰めて１７０個の差をなくす。
・その後、８個入りの箱(図のウとエ)に残りのお菓子を全部詰める。
という作戦で、Ａ５２０個とＢ３５０個をすべて箱へ詰めることにします。
※ 画像はすべて、クリックすると拡大します。
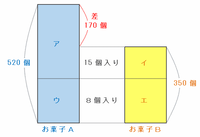
１５個入りの箱はＡ１０個とＢ５個を詰めるので、１箱完成させるごとに、ＡとＢの残りの差は１０－５＝５個ずつ縮まっていきます。
そのペースで１７０個の差をゼロにするには、次の図のように１５個入りの箱を１７０÷５＝３４箱完成させればＯＫです。
また、その時点でお菓子Ａは１０×３４＝３４０個、Ｂは５×３４＝１７０個使ったので、残りのお菓子はＡが５２０－３４０＝１８０個、Ｂも３５０－１７０＝１８０個になっています。
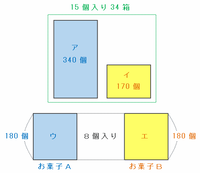
８個入りの箱はお菓子ＡとＢ(上の図のウとエ)を４個ずつ詰めるので、１８０÷４＝４５箱必要です。
以上から、１５個入りの箱は３４箱、８個入りの箱は４５箱できました。
(２)
さっきの問題と同じように、まずはお菓子ＡとＢの合計である９００個を７：８の割合に比例配分してみると、
・お菓子Ａ→９００×１５分の７＝４２０個
・お菓子Ｂ→９００×１５分の８＝４８０個
となります。
つまり、どちらのお菓子の数も一の位が「０」なので、
・１５個入りの箱→２箱セットにすると、Ａは１０×２＝２０個、Ｂは５×２＝１０個となり、どちらも一の位が「０」になる
・９個入りの箱→１０箱セットにすると、Ａは３×１０＝３０個、Ｂは６×１０＝６０個となり、どちらも一の位が「０」になる
という発想をもとにして、２種類の箱をそれぞれ次の図のような１セットにします。
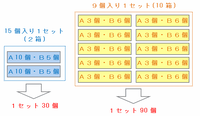
上の図の９個入り１セット(１０箱)にはお菓子が９×１０＝９０個入っているので、それを１０セット用意すれば、お菓子の合計はちょうど９０×１０＝９００個になります。
ただ、「９個入り１０セット」と「実際のお菓子の数」をＡとＢでそれぞれ比べてみると、
・お菓子Ａ→「９個入り１０セット」の中にはＡが３×１０×１０＝３００個、実際のＡは４２０個
・お菓子Ｂ→「９個入り１０セット」の中にはＢが６×１０×１０＝６００個、実際のＢは４８０個
なので、次の図のようにＡは４２０－３００＝１２０個余り、Ｂは６００－４８０＝１２０個足りないという状態になってしまいます。
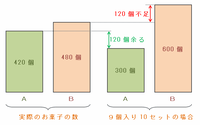
つまり、上の図の状態からＡとＢの数を１２０個逆転させればＯＫなので、９個入りセットを１５個入りセットと交換してその差をうまく調整します。
９個入り１セットはお菓子が９０個なので、次の図のように１５個入り３セットと１回交換すると、
・お菓子Ａ→９個入り１セットはＡを３×１０＝３０個、１５個入り３セットはＡを１０×６＝６０個使うので、さっき余ってたＡが６０－３０＝３０個余分に使われる。
・お菓子Ｂ→９個入り１セットはＢを６×１０＝６０個、１５個入り３セットはＢを５×６＝３０個使うので、さっきの不足分が６０－３０＝３０個ずつ埋まる。
ことから、下の図のような交換を１回行うごとに、さっきの１２０個の差は３０個ずつ縮まっていくことが分かります。
※ Ａは余りが３０個ずつ消費され、Ｂは不足分が３０個ずつ埋まっていく。
つまり、上の図のような交換を１２０÷３０＝４回行えば、「Ａが１２０個余った」と「Ｂが１２０個足りない」状態が同時に解消されるので、
・上の図の１５個入り３セット(６箱)は４つ→つまり、１５個入りの箱は６×４＝２４箱
・上の図の９個入り１セット(１０箱)は１０－４＝６つ→つまり、９個入りの箱は１０×６＝６０箱
のように振り分けたとき、お菓子ＡとＢがピッタリと箱におさまります。
PR
