けんじ君は、ボールペンをまとめて買うことにしました。１本の値段は、５０本目までは９６円、５１本目から１００本目までは９５円、１０１本目からは８５円です。たとえば、１０５本買うと、９９７５円になります。次の問いに答えなさい。
(１) １７５本買うと、１本あたり何円になりますか。
(２) 何本買うと、１本あたり８７円になりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
とりあえず答えを出すだけでＯＫなら、
・１～５０本目まで(５０本)→９６×５０＝４８００円
・５１～１００本目まで(５０本)→９５×５０＝４７５０円
・１０１～１７５本目まで(７５本)→８５×７５＝６３７５円
なので、１本あたりの値段は(４８００＋４７５０＋６３７５)÷１７５＝９１円で終わりです。
ただ、そのやり方しか使えないと次の問題で困っちゃうので、面積図を利用して平均の値段を求めてみます。
最初の５０本は１本あたり９６円、次の５０本は１本あたり９５円なので、１～１００本目までの平均価格は(９６＋９５)÷２＝９５.５円です。
※ どちらも本数が同じ５０本なので、「÷２」で平均価格が分かる。
つまり、「１本９５.５円のボールペン１００本」と「１本８５円のボールペン７５本」の平均価格を求めればＯＫなので、次のような面積図を利用して答えを求めてみます。
※ 画像はすべて、クリックすると拡大します。
上の図のアがイへ流れ込むことによって全体の高さが等しくなるので、そのときの高さ(図の赤い線)が全体の平均価格を表しています。
また、上の図の長方形アとイの面積比は等しく、横の長さの比はア：イ＝１００本：７５本＝４：３なので、アとイの高さの比はその逆比である３：４になります。
※ アとイの面積を等しくするには、横の長さをたての長さの逆比にすればＯＫ。
つまり、上の図の３＋４＝７(アとイの高さの比の合計)が、１００本と７５本の平均価格の差である９５.５－８５＝１０.５円にあたるので、高さの比の１は１０.５÷７＝１.５円です。
平均価格は、８５円よりも比の４だけ高いので、答えは８５＋１.５×４＝９１円になります。
また、９５.５円よりも比の３だけ低いことから、９５.５－１.５×３＝９１円と求めてもＯＫです。
(２)
１～１００本目までの平均価格が９５.５円であることは変わりないので、「１本９５.５円のボールペン１００本」と「１本８５円のボールペン□本」の平均価格が８７円となる次のような面積図を利用して答えを求めます。
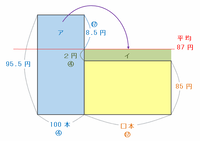
全体の平均価格は８７円なので、上の図のアの高さは９５.５－８７＝８.５円、イの高さは８７－８５＝２円です。
つまり、長方形アとイの高さの比は８.５円：２円＝１７：４なので、アとイの横の長さの比はその逆比である４：１７になります。
上の図の１００本：□本＝４：１７のとき、□には１００×１７÷４＝４２５本があてはまるので、平均価格が８７円になるまでに買ったボールペンの本数は、全部で１００＋４２５＝５２５本になります。
PR
