袋の中に数を書いたいくつかの玉が入っています。この袋に、
『２個の玉を袋の中から取って、２つの数の平均を書いた玉１個を袋に戻す』
という操作を、袋に入っている玉が１個になるまで繰り返し行います。
例えば、袋に「１」、「２」、「３」と書いた３個の玉が入っているとき、最初に２と３の玉を取った場合には、「１」と「２.５」の２個の玉になり、最後に「１.７５」の玉が残ります。
次の問いに答えなさい。
(１)
連続する３つの数「３」、「４」、「５」を書いた３個の玉が入っている袋に、操作を繰り返し行いました。最後に残る玉に書かれた数は何ですか。考えられるもののうち、最も小さい数を答えなさい。
(２)
連続する４つの整数を書いた４個の玉が入っている袋に、操作を繰り返し行います。このとき、最後に残る玉に書かれた数として考えられるもののうち、最も小さい数は５.８７５です。
(ア) はじめに袋に入っていた玉に書かれた４つの整数は何ですか。４つの整数すべてを書きなさい。
(イ) 最後に残る玉に書かれた数として考えられるもののうち、最も大きい数は何ですか。
(ウ) 最後に残った玉に書かれた数が６.８７５でした。最初に取った２個の玉に書かれた数は何ですか。考えられる数の組み合わせを、(○と△)のようにして、すべて答えなさい。
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
(１)
最後の玉に書かれた数をなるべく小さくするためには、
・いちばん小さい数は最後まで残しておく
・大きい２つの数を平均して１つの玉に変えてしまう
という２つのルールがあります。
そのルールにしたがって「３」、「４」、「５」で作業を進めてみると・・・
１回目→大きい２つの数を平均して、(４＋５)÷２＝４.５の玉に変えます。
２回目→残しておいた「３」との平均は、(３＋４.５)÷２＝３.７５になります。
※ この作業を図に表してみると、次のようになります。
(２)の(ア)
４つの連続した整数を小さい順にＡ、Ｂ、Ｃ、Ｄとおくと、最後の玉に書かれた数をなるべく小さくするためには、
１回目→ＣとＤの平均を求める。その答えをＥとする。
２回目→ＢとＥの平均を求める。その答えをＦとする。
３回目→ＡとＦの平均を求める。その答えが５.８７５である。
という流れで作業を進めていきます。
その流れをさっきと同じように図に表してみると、次のようになります。
上の図のＡからＦまでは１＋０.７５＝１.７５はなれているので、図の？は１.７５÷２＝０.８７５になります。
Ａは最後の平均である５.８７５よりも０.８７５小さい数である５になるので、連続する４つの整数は「５」、「６」、「７」、「８」になります。
(２)の(イ)
「５」、「６」、「７」、「８」の最後の平均をなるべく大きくするためには、いちばん大きい数である「８」を最後まで残しておいて、小さい数の平均から順に求めていけばＯＫです。
１回目→(５＋６)÷２＝５.５
２回目→(５.５＋７)÷２＝６.２５
３回目→(６.２５＋８)÷２＝７.１２５になります。
(２)の(ウ)
最後(３回目)の平均である６.８７５を手掛かりにして、２回目の平均→１回目の平均の順に過去へさかのぼっていきます。
３回目の平均である６.８７５＝(５から８までのどれか１つ＋２回目の平均)÷２なので、とりあえず５から８までのうち、好きな数を１つ選んでください。日ごろの行いが正しい人なら正解の数が一発で選べるはずです(笑)
さっそく「５」を選んでみると、次のような図になります。
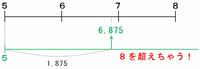
最後の平均である６.８７５と左はしの５との差は１.８７５なので、右はしの数(つまり２回目の平均)は６.８７５＋１.８７５＝８.７５になってしまいます。
８までしかないのに平均がそれを超えちゃうのは、さすがにおかしいですね。
というわけで、気を取り直して「６」を選んでみると次のような図になります。
３回目→(６＋７.７５)÷２＝６.８７５ つまり、２回目の平均は７.７５
２回目→(７＋□)÷２＝７.７５ つまり、１回目の平均は７.７５×２－７＝８.５
はい、これも１回目の平均が８を超えてしまうのでダメですね。
こんなことでくじけずに、今度は「７」を選んで再挑戦です。
３回目→(６.７５＋７)÷２＝６.８７５ つまり、２回目の平均は６.７５
２回目→(□＋８)÷２＝６.７５ つまり、１回目の平均は６.７５×２－８＝５.５
１回目→５.５は、まだ選んでいない「５」と「６」の平均になっている。
つまり、１回目に「５」と「６」の玉を選んだ場合に、最後の平均が６.８７５になることが分かります。
では最後に「８」を選んで、同じように調べてみましょう。
３回目→(５.７５＋８)÷２＝６.８７５ つまり、２回目の平均は５.７５
２回目→(５＋□)÷２＝５.７５ つまり、１回目の平均は５.７５×２－５＝６.５
１回目→６.５は、まだ選んでいない「６」と「７」の平均になっている。
つまり、１回目に「６」と「７」の玉を選んだ場合でも、最後の平均が６.８７５になることが分かります。
以上から、求める組み合わせは(５と６)、(６と７)の２通りになります。
PR
