次の図１のように２つの直角三角形ＡＢＣとＡＣＤを組み合わせてできた四角形ＡＢＣＤについて、次の問いに答えなさい。ただし、必要であれば、図１を４つ組み合わせた図２を用いなさい。
※ 画像はすべて、クリックすると拡大します。
【補足】
・辺ＡＢと辺ＢＣの長さの合計は８.５㎝です。
・辺ＣＤは辺ＤＡよりも１.５㎝長いです。
・辺ＡＢは辺ＢＣよりも短いです。
(１) 三角形ＡＢＣの面積を求めなさい。
(２) 四角形ＡＢＣＤの面積を求めなさい。
(３) ＡＢの長さを求めなさい。ただし、ＡＢ、ＢＣのどちらかの長さは整数になります。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
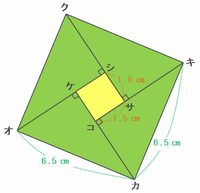
次の図の正方形アイウエの一辺の長さは、三角形ＡＢＣの辺ＡＢと辺ＢＣの和と等しいので８.５㎝になります。
また、緑色の正方形クオカキの一辺の長さは三角形ＡＢＣの辺ＡＣと等しいので６.５㎝です。
※ 画像はすべて、クリックすると拡大します。
上の図の正方形アイウエの面積は８.５×８.５＝７２.２５㎠、そして緑色の正方形クオカキの面積は６.５×６.５＝４２.２５㎠なので、その差は７２.２５－４２.２５＝３０㎠です。
その３０㎠は上の図の４すみにある青い４個の三角形の面積なので、１個分の面積(つまり三角形ＡＢＣの面積)は３０÷４＝７.５㎠になります。
(２)
次の図の黄色い正方形ケコサシの一辺の長さは、三角形ＡＣＤの辺ＣＤと辺ＤＡの差にあたるので１.５㎝だと分かります。
したがって、正方形ケコサシの面積は１.５×１.５＝２.２５㎠になります。
正方形クオカキの面積は４２.２５㎠なので、黄色い正方形ケコサシとの面積の差は４２.２５－２.２５＝４０㎠になります。
その４０㎠は上の図にある緑色の三角形４個分の面積にあたるので、１個分の面積(つまり三角形ＡＣＤの面積)は４０÷４＝１０㎠です。
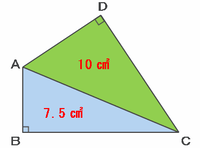
つまり次の図のように、三角形ＡＢＣの面積は７.５㎠、そして三角形ＡＣＤの面積は１０㎠なので、四角形ＡＢＣＤの面積は７.５＋１０＝１７.５㎠になります。
(３)
三角形ＡＢＣの辺ＡＢの長さを□㎝、辺ＢＣの長さを△㎝とおくと、面積を求める式は□×△÷２＝７.５㎠と表せるので、□×△の答えは７.５×２＝１５となります。
この□と△にあてはまる数には、
・□は△より小さい
・□と△のどちらかは整数である
・□と△の合計は８.５である
という３つの条件があるので、整数となる数は８以下、そしてもう一方の数は小数第一位が５となる数であることが分かります。
【補足】
次の「(整数ア)＋(イ.ウ)＝８.５」の筆算を表した図を見れば分かるように、答えの小数第一位にある５は「イ.ウ」のウがそのまま来るので、「イ.ウ」は「イ.５」と表せます。
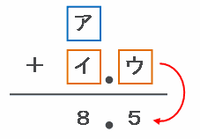
(整数ア)×(イ.５)＝１５という式は、１５÷(整数ア)＝(イ.５)と書き換えることができます。
その割り算の式の(整数ア)には８以下の整数があてはまるのですが、その中で１５を割ったときの商の小数第一位が５となるのは、「１５÷２＝７.５」、「１５÷６＝２.５」のときです。
つまり、(整数ア)の候補は「２」と「６」の２通りが考えられるのですが、
・(整数ア)が２のとき、(イ.５)は７.５。その２つの数の和は２＋７.５＝９.５
・(整数ア)が６のとき、(イ.５)は２.５。その２つの数の和は６＋２.５＝８.５
となることから、３つの条件のうちの１つである「２つの数の和は８.５」を満たしているのは６と２.５の組み合わせのときであることが分かります。
また、辺ＡＢの長さは辺ＢＣよりも短いので、辺ＡＢの長さは２.５㎝になります。
PR
