４枚のカードＡ、Ｂ、Ｃ、Ｄがあり、それぞれ表と裏に次のように数字が書いてあります。
※ 画像はクリックすると拡大します。
この中からカード３枚を順に並べて、３けたの整数を作ります。次の問いに答えなさい。
(１)
Ａ、Ｂ、Ｃの３枚のカードを順に並べるとき、偶数は何通りできますか。
(２)
Ａ、Ｂ、Ｃ、Ｄの４枚のカードから３枚を選んで順に並べるとき、３の倍数は何通りできますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
Ａ、Ｂ、Ｃの３つのカードを並べて３ケタの偶数を作る場合、一の位には「０・２・４」のいずれかが来ます。
【一の位に０が来る場合】
次の図のように、一の位にＡのカードの表面にある０が来る場合、百の位はＢまたはＣのカードの両面にある「２・３・４・５」のいずれかがあてはまります。
また、仮に百の位にＢのカードをあてはめたとすると、十の位にはＣのカードの両面にある「４・５」のどちらかがあてはまります。
逆に百の位にＣのカードをあてはめると、十の位にはＢのカードの両面にある「２・３」のどちらかがきます。
※ 画像はすべて、クリックすると拡大します。
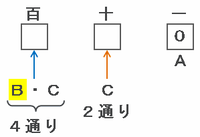
つまり一の位が０の場合、百の位にあてはめる数字の選び方が４通り(ＢまたはＣの両面にある４つの数のどれか)、そして十の位の数字は２通り(百の位で使わなかったカードの両面にある数のどちらか)なので、３けたの偶数「□□０」の作り方は４×２＝８通りになります。
【一の位が２または４の場合】
とりあえず一の位にＢのカードの表面にある２をあてはめてみると、百の位にＡとＣのどちらのカードを使うのかによって話の続きが変わってきます。
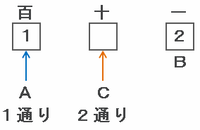
たとえば百の位にＡのカードを使う場合、次の図のようにＡのカードは裏面の１しか使えません。
※ いちばん上の位に０は使えないから。
また、十の位にはＣの両面にある「４・５」のどちらかがあてはまるので、３けたの偶数「ＡＣ２」の作り方は１×２＝２通りになります。
次は百の位にＣのカードを使う場合を考えてみると、百の位にはＣの両面にある「４・５」のどちらかが、そして十の位にはＡの両面にある「０・１」のどちらかがあてはまります。
つまり、３けたの偶数「ＣＡ２」の作り方は２×２＝４通りになります。
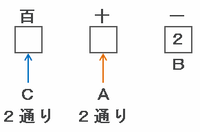
以上から、一の位が２の場合、３けたの偶数は全部で２＋４＝６通り作れます。
ここまでの流れから、
・一の位が０のとき→３けたの偶数の組み合わせは全部で８通り
・一の位が２のとき→３けたの偶数の組み合わせは全部で６通り
・一の位が４のとき→一の位が２のときと同じく６通り
であることが分かるので、３けたの偶数は全部で８＋６×２＝２０通りできます。
(２)
３の倍数には「各位の和が３の倍数になる」という特徴があるので、まずは０から７までの中から３つの数を選び、その合計が３の倍数になるときを考えてみます。
０から７までの中から３つの数を選んだときの和は、最も小さい場合が０＋１＋２＝３、最も大きい場合が５＋６＋７＝１８です。
ただし、「０・１」と「６・７」はそれぞれ同じカードの両面にある数なので、実際には３つの数の合計が３や１８になることはあり得ません。
そこで、３つの数の合計が３の倍数のうち「６・９・１２・１５」になる組み合わせを探してみると、次のようになります。
・６になる場合→(０・２・４)
・９になる場合→(０・３・６)、(０・２・７)、(１・２・６)、(１・３・５)
・１２になる場合→(０・５・７)、(１・４・７)、(１・５・６)、(２・４・６)
・１５になる場合→(３・５・７)
このうち、たとえば(０・２・４)のように０が使われている組み合わせの場合、百の位には０が使えないので「２・４」のどちらか(仮に２を選んだとする)、十の位は「０・４」のどちらか(仮に０を選んだとする)、そして一の位は最後に残った「４」となることから、３けたの数は全部で２×２×１＝４通りできます。
一方、(１・２・６)のように０が使われていない場合は特に制限がないので、百の位には「１・２・６」のどれか(仮に１を選んだとする)、十の位は「２・６」のどちらか(仮に２を選んだとする)、そして一の位は最後に残った「６」となることから、３けたの数は全部で３×２×１＝６通りできます。
さっき見つけた３の倍数になる組み合わせのうち、０を使う場合が４通り、０を使わない場合が６通りあるので、答えは４×４＋６×６＝５２通りになります。
PR
