校庭に、たて、横１ｍの間隔でラインが次の図のように引かれています。ラインが交わったところに生徒２５人が、たて、横５人ずつ図のように並んでいます。●印は生徒を表します。先生もラインが交わったところに立つとします。ただし、生徒や先生の大きさは考えないものとします。次の各問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１)
①の地点にいる先生には、見える生徒と、重なって見えない生徒がいます。全部で何人の生徒が見えますか。
(２)
①の地点に１人の先生がいて、さらにもう１人の先生が、②から⑧のどこに立てば、２人の先生ですべての生徒を見ることができますか。考えられるすべての地点を答えなさい。
(３)
①と②を通るラインで、①の左側に１人の先生が立って生徒全員を１人の先生で見ることができます。この地点の中で最も①に近いところは、①から左へ何ｍの地点になりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
①の地点から次の図のように３本の直線を引いてみると、赤い●の地点にいる生徒は青い●の地点にいる生徒と重なるため、先生には見えません。
※ 画像はすべて、クリックすると拡大します。
生徒は全部で２５人、赤い●の地点にいる生徒は６人なので、①の地点から見える生徒は全部で２５－６＝９人になります。
(２)
さっきの問題で見つけた６個の赤い●が死角にならない地点を見つけます。
次の図のように、④、⑤、⑥の地点は真横の青い死角となる部分に赤い●があるのでアウトです。
また、次の２つの図のように、②と⑧の地点は青い●の生徒のせいで赤い５個の●が死角となるのでやはりアウトです。
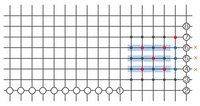
最後に残った③と⑦の地点は、次の２つの図のように斜めと真横の死角に赤い●が１つも入っていないのでＯＫです。
※ 緑色の矢印と最初にぶつかるのが赤い●の場合、それは死角にはなりません。
以上から、もう１人の先生が立つ地点は③と⑦になります。
(３)
①の地点から左へ７ｍ先の○までは、次の図のように「底辺：高さ＝２：１」の三角形の斜辺を伸ばした直線の先に死角ができてしまいます。
今度は①から左へ８ｍの地点にある○から緑色の矢印を伸ばしてみると、次の図のように「底辺：高さ＝２：１」の三角形の斜辺なら死角はできないのですが、「底辺：高さ＝３：１」の三角形の斜辺だと１か所だけ死角ができてしまいます。
次は①から左へ９ｍの地点にある○から緑色の矢印を伸ばしてみると、底辺と高さが２：１、３：１、４：１の三角形の斜辺を下の図のように伸ばしても死角はできません。
また、生徒の間隔は最大でも４ｍなので、底辺と高さが５：１とか６：１の場合を調べる必要はありません。
以上から、条件にあてはまる最も近い地点は、①から左へ９ｍ先の○になります。
【補足】
「高さが２ｍの場合は考えなくてもいいの？」と思ったあなた、なかなか鋭いですね。
でも、例えば「底辺：高さ＝４：２」の場合は２：１と同じ直線になるので考えなくてＯＫだし、「底辺：高さ＝３：２」だと、次の図のように緑色の直線が生徒たちの場所よりも上を通過してしまうので、考える必要はありません。
PR
