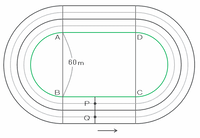
次の図のようなトラックがあります。最も内側の緑色の線は長方形ＡＢＣＤと直径６０ｍの半円２つでできていて、周の長さは４００ｍです。このとき、次の問いに答えなさい。ただし、円周率は３.１４とします。
※ 画像はクリックすると拡大します。
①
辺ＡＤの長さは何ｍですか。
②
あきら君とたかし君はこのトラックで、競走をすることにしました。２人は図の矢印の向きに同じ距離を走ります。コースの幅は１ｍで、あきら君は内側のコースを１周し、たかし君は外側のコースを走ります。２人ともそれぞれのコースのちょうど真ん中(図の点線部分)を走るものとし、図の点線部分は長方形と半円２つでできた図形です。あきら君のスタート地点とゴール地点は図の点Ｐの位置とし、たかし君のゴール地点は図の点Ｑの位置とします。ＰＱとＡＢは平行です。たかし君は点Ｑより何ｍ前でスタートすればよいですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
①
緑色のコース１周は、次の図のように「直径６０ｍの半円２つ(つまり円１個分)」と「直線ＡＤ＋ＢＣ」からできています。
※ 画像はすべて、クリックすると拡大します。
直径６０ｍの円周の長さは６０×３.１４＝１８８.４ｍです。また、コース１周の長さは４００ｍなので、直線ＡＤとＢＣの長さの合計は４００－１８８.４＝２１１.６ｍです。
直線ＡＤとＢＣは同じ長さなので、ＡＤの長さは２１１.６÷２＝１０５.８ｍになります。
②
コースの内側でも外側でも直線２本の長さに変わりはないので、２人が走るコースの半円２つ分の長さを比べてみればＯＫです。
次の図のように、あきら君が通るコースは緑色の線よりも両側に１÷２＝０.５ｍずつふくらんでいるので、青い点線の半円の直径は６０＋０.５×２＝６１ｍになります。
したがって、あきら君が走る半円２つ分の長さの合計を求める式は「６１×３.１４」と表せます。
次の図のように、たかし君が通るコースは緑色の線よりも両側に１＋０.５＝１.５ｍずつふくらんでいるので、オレンジ色の半円の直径は６０＋１.５×２＝６３ｍになります。
したがって、たかし君が走る半円２つ分の長さの合計を求める式は「６３×３.１４」と表せます。
「６３×３.１４」と「６１×３.１４」との差は(６３－６１)×３.１４＝２×３.１４を計算すれば求められるので、たかし君が点Ｑよりも２×３.１４＝６.２８ｍ先からスタートすれば、２人の１周の長さが等しくなります。
PR
