１が１２個並んだ整数１１１１１１１１１１１１の約数について、次の問いに答えなさい。
(１)
次の図の答えの欄の数のうち約数であるものには○、そうでないものには×を左の空欄に書きなさい。
※ 画像はクリックすると拡大します。
(２)
すべての位の数字が０か１であるような約数のうち、(１)で答えた数以外のものを７個書きなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
１とその数自体は必ず約数なので、とりあえず「１」と「１１１１１１１１１１１１」の欄にはどちらも○があてはまります。
また、１２の約数は「１・２・３・４・６・１２」なので、１２個並んだ「１」を２個ずつ、３個ずつ、４個ずつ、６個ずつのグループに分けることができます。
たとえば次の図のように、１２個の「１」を２個ずつのグループに分けた場合、いちばん右側にある「１１」は１１×１、そのとなりの「１１」は１１×１００、そのとなりの「１１」は１１×１００００、・・・のように、すべてのグループを「１１×□」の形で表すことができます。
※ 画像はすべて、クリックすると拡大します。
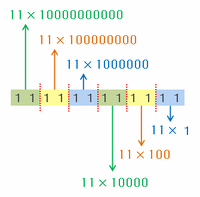
つまり、１２けたの整数「１１１１１１１１１１１１」は１１の倍数なので、解答欄の「１１」のところに○を書き込みます。
また、次の図のように１２個の「１」を３個ずつ、４個ずつ、６個のグループに分けることもできるので、１２けたの整数「１１１１１１１１１１１１」は１１１、１１１１、１１１１１１の倍数であることが分かります。
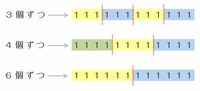
以上から、解答欄には次の図のように○または×をつけます。この図を見れば分かるように、「１」の数が１２の約数だけある欄に○を、それ以外の欄には×を書き込めばＯＫです。
(２)
１２個並んだ「１」を次の図のように２個ずつのグループに分けると、Ａ～Ｆはどれも「１１×□」という形で表すことができます。
それらを下の図のように縦に並べて筆算してみると「１１×１０１０１０１０１０１」となるので、「１０１０１０１０１０１」は１２けたの整数「１１１１１１１１１１１１」の約数であることが分かります。
また、１２個並んだ「１」を次の図のように３個ずつのグループに分けると、Ａ～Ｄはどれも「１１１×□」という形で表すことができます。
それらを下の図のように縦に並べて筆算してみると「１１×１００１００１００１」となるので、「１００１００１００１」も約数のひとつであることが分かります。
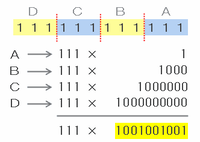
１２個並んだ「１」を次の図のように４個ずつ分けた場合、６個ずつ分けた場合についても同じように考えてみると、
・４個ずつ→１１１１１１１１１１１１＝１１１１×１０００１０００１
・６個ずつ→１１１１１１１１１１１１＝１１１１１１×１０００００１
となるので、１０００１０００１と１０００００１も約数になります。
今のところ、問題文の条件にあてはまる約数がまだ４個しか見つかっていないので、１２個並んだ「１」の分け方を工夫して他の約数を見つけてみます。
１２個並んだ「１」を、次の図のように１個飛ばしで２個ずつのペアにしてみると、Ａ～Ｆはすべて「１０１×□」という形で表すことができます。
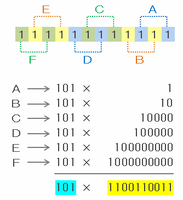
それらを下の図のように縦に並べて筆算してみると「１０１×１１００１１００１１」となるので、「１０１」と「１１００１１００１１」も約数であることが分かります。
また、１２個並んだ「１」を、次の図のように２個飛ばしで２個ずつのペアにしてみると、Ａ～Ｆはすべて「１００１×□」という形で表すことができます。
それらを下の図のように縦に並べて筆算してみると「１００１×１１１０００１１１」となるので、「１００１」と「１１１０００１１１」も約数になります。
もし１２個並んだ「１」を、次の図のように１個飛ばしで３個ずつのペアに分けると、Ａ～Ｄはすべて「１０１０１×□」という形で表すことができます。
それらを下の図のように縦に並べて筆算してみると「１０１０１×１１００００１１」となるので、「１０１０１」と「１１００００１１」も約数です。
以上から、１２けたの整数「１１１１１１１１１１１１」の約数のうち、１と０の組み合わせで作れるものは、
・１０１０１０１０１０１
・１００１００１００１
・１０００１０００１
・１０００００１
・１０１
・１１００１１００１１
・１０１０１
・１１００００１１
などがあるので、そのうちの７個を答えれば正解となります。
PR
