電車の線路沿いの道を時速９㎞の速さで進んでいる人が１５分ごとに電車に追い越され、９分ごとに向かいから来る電車とすれ違いました。電車の速さはどちらも一定で、電車は同じ間隔で運転されているとすると、その速さは時速( )㎞です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずはこの人が進む速さを分速に直しておくと、９×１０００÷６０＝分速１５０ｍになります。
次の図のように、左から右へ進んでいる人が１２時ちょうどにＡ地点で電車１号に追いつかれたとします。
左からは電車２号が着々と近づいているので、Ａ地点からそのまま右へ進めば追いつかれ、方向転換して左へ進めば向かい合わせの形ですれ違います。
※ 画像はすべて、クリックすると拡大します。
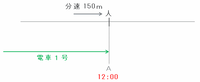
この人は電車と向かい合わせで進むと９分ごとにすれ違うので、もし１２時ちょうどにこの人が左へ向かって進み始めると、次の図のようにＡ地点から左へ１５０×９＝１３５０ｍ離れたＢ地点で、１２時９分に電車２号と出会います。
※ つまり、電車２号は１２時９分にはＡ地点から左へ１３５０ｍの地点にいる。
また、この人は電車と同じ方向へ進むと１５分ごとに追いつかれるので、もしこの人が１２時ちょうどから後も右へ進み続けると、次の図のようにＡ地点から右へ１５０×１５＝２２５０ｍ離れたＣ地点で、１２時１５分に電車２号に追いつかれます。
※ つまり、電車２号は１２時１５分にはＡ地点から右へ２２５０ｍの地点にいる。
つまり次の図のように、電車２号は１２時９分から１２時１５分までの６分間で、Ｂ地点からＣ地点までの１３５０＋２２５０＝３６００ｍ進むことが分かるので、この電車の速さは３６００÷６＝分速６００ｍです。
最後に分速６００ｍを時速に直しておくと、６００×６０÷１０００＝時速３６㎞になります。
PR
