図のような長方形ＡＢＣＤにおいて、点ＨはＡＦのまん中の点です。色が塗られたイの面積はアの面積の半分で、ウの面積はイの面積の半分です。次の問いに答えなさい。
※ 画像はすべて、クリックすると拡大します。
(１) アの部分の面積を求めなさい。
(２) ＦＧの長さを求めなさい。
(３) ＥＨとＨＤの長さの比を、できるだけ小さい整数の比で表しなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
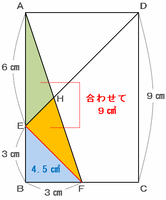
まずは四角形ＥＢＦＨの面積を直線ＥＦで２つに分け、三角形ＥＢＦとＥＦＨの面積を別々に求めてみると・・・
・三角形ＥＢＦの面積→３×３÷２＝４.５㎠
・三角形ＡＥＦの面積→底辺をＡＥとすると高さがＢＦにあたるので、６×３÷２＝９㎠
になります。
※ 画像はすべて、クリックすると拡大します。
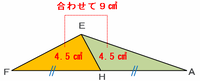
今度は下の図のように、三角形ＡＥＦを辺ＦＡが底辺になるようにクルッと時計回りに回転させてみると、点Ｈは辺ＦＡの真ん中にあるので、辺ＦＨと辺ＨＡの長さは同じです。
つまり、下の２つの三角形は底辺と高さが等しいので、面積はどちらも９÷２＝４.５㎠になっています。
つまり、三角形ＥＢＦとＥＦＨの面積はどちらも４.５㎠なので、求めるアの面積は４.５×２＝９㎠になります。
(２)
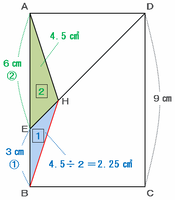
次の図の三角形ＨＡＥとＨＢＥは、底辺をそれぞれ辺ＡＥ、辺ＥＢと考えると高さが同じなので、この２つの三角形の面積比は底辺の長さの比と等しくなります。
つまり、この２つの三角形の面積比はＨＡＥ：ＨＢＥ＝６㎝：３㎝＝２：１となるので、三角形ＨＢＥの面積はＨＡＥの面積の半分であることが分かります。
また、下の図の三角形ＨＡＥの面積は４.５㎠(さっきの問題で確認済み)なので、三角形ＨＢＥの面積は４.５÷２＝２.２５㎠になります。
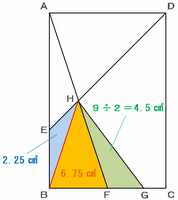
次の図の四角形ＥＢＦＨの面積は９㎠、三角形ＨＥＢの面積は２.２５㎠なので、三角形ＨＢＦの面積は９－２.２５＝６.７５㎠です。
また、三角形ＨＦＧの面積は四角形ＥＢＦＨの半分(問題文に書いてあります)なので、９÷２＝４.５㎠です。
したがって、下の図の三角形ＨＢＦとＨＦＧの面積比は、ＨＢＦ：ＨＦＧ＝６.７５㎠：４.５㎠＝３：２になります。
下の図の三角形ＨＢＦとＨＦＧは高さが同じなので、底辺の長さの比は面積比と等しくなっています。
つまりＢＦ：ＦＧ＝３：２なのですが、ＢＦの長さである比の③は３㎝なので、比の①は１㎝であることが分かります。
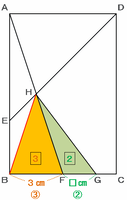
ＦＧの長さは比の②にあたるので、答えは２㎝になります。
(３)
まずは下の図の辺ＧＣの長さを確認しておくと、問題文に「ウの面積はイの面積の半分」とあるので、辺ＧＣの長さは辺ＦＧの長さの半分になっています。
したがって、辺ＧＣの長さは２÷２＝１㎝になります。
このとき、下の図の辺ＢＣは３＋２＋１＝６㎝、そして辺ＢＦの長さは３㎝なので、点Ｆは辺ＢＣの真ん中の点であることも分かります。
次は下の図のように、辺ＢＣと垂直な赤い線を点Ｆから真上に向けて伸ばしてみると、その線はやがて直線ＥＤとぶつかります。
この赤い線ＩＦは辺ＥＢと辺ＤＣの真ん中にあるので、長さは２つの辺の長さの平均になっています。
したがって、下の図の赤い直線ＩＦの長さは(３＋９)÷２＝６㎝になります。
このとき、下の図の三角形ＡＥＨと三角形ＦＩＨは合同になる(辺ＡＥと辺ＩＦの長さが等しく、内角も同じ)ので、辺ＥＨと辺ＨＩの長さはどちらも①と表せます。
今度は下の図のオレンジ色と緑色の直線に注目してみます。
赤い直線ＩＦは辺ＥＢと辺ＤＣの真ん中にあるので、点Ｉは直線ＥＤの中央にぶつかっています。
つまり辺ＥＩと辺ＩＤの長さは等しいので、どちらの辺の長さも比の①＋①＝②と表せます。
以上から、辺ＥＨの長さは比の①、辺ＨＤの長さは比の①＋②＝③と表せることが分かったので、この２つの辺の長さの比はＥＨ：ＨＤ＝１：３になります。
PR
