気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
08/16
Mon
2010
灘2010【6】 ☆組み合わせ・整数の性質☆
4けたの整数ABCDを考えます。ただし、A、B、C、Dには同じ数字があってもよいこととします。数字の並びを逆にしたDBCAがABCDより大きい4けたの整数となるようなABCDは全部で( ア )個あります。また、DCBAがABCDと等しい4けたの整数となるようなABCDすべての合計は( イ )です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(ア)
4けたの数DCBAがABCDよりも大きくなるのは、
① 「DCBA」の千の位にあるDが、「ABCD」の千の位にあるAよりも大きいとき
② 千の位にあるDとAは等しく、百の位にあるCがBより大きいとき
の2通りが考えられます。
【補足】
「あれ?十とか一の位で数の大きさが決まる場合もあるんじゃないの?」と思ったあなた。
千の位にあるDとAが等しく、百の位にあるCとBも同じなのに、十の位のBとCや一の位のAとDの大きさが違うなんてありえないですよね。
だから、DCBAとABCDの大きさが異なる場合は、必ず千の位または百の位で決着がついているはずなのです。
というわけで、ここからはさっきの①と②の場合でABCDがそれぞれ何通りできるのかを考えてみます。
【千の位にあるDがAよりも大きい場合】
4けたの数DCBAとABCDを次の図のように並べてみると、千の位にあるDがAより大きければ、残りのBとCには何があってもかまいません。
また、DやAはいちばん上の位にあてはまる数なので「0」を使うことはできません。
※ 画像はすべて、クリックすると拡大します。
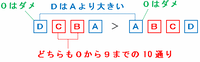
DがAより大きくなる組み合わせは、D=2ならA=1、D=3ならA=1または2、D=4ならA=1か2か3、・・・のようにD=9まで数えていくと、全部で1+2+3+4+5+6+7+8=36通りあります。
DがAより大きくなる組み合わせは、D=2ならA=1、D=3ならA=1または2、D=4ならA=1か2か3、・・・のようにD=9まで数えていくと、全部で1+2+3+4+5+6+7+8=36通りあります。
また、BとCにはそれぞれ0から9までの10個の数を好きにあてはめればOKなので、その組み合わせは次の図のように10×10=100通りあります。
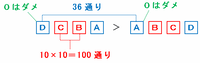
したがって、DがAより大きい場合のABCDの組み合わせは全部で36×100=3600通りになります。
【千の位のDとAは等しく、百の位にあるCがBより大きい場合】
次の図のように千の位にあるDとAが等しいとき、残りのCがBより大きければDCBAの方が大きい数になります。

その場合、DとAにあてはまる数の組み合わせは(1・1)から(9・9)までの9通りになります。
また、C=1ならB=0、C=2ならB=0または1、C=3ならB=0か1か2、・・・のようにC=9のときまで数えていくと、その組み合わせは全部で1+2+3+4+5+6+7+8+9=45通りあります。
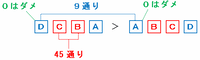
したがって、DとAが等しい場合のDCBAの組み合わせは全部で9×45=405通りです。
したがって、DとAが等しい場合のDCBAの組み合わせは全部で9×45=405通りです。
以上から、DCBAがABCDよりも大きくなる場合は全部で3600+405=4005通りになります。
(イ)
ABCDとDCBAを等しくするためには、次の図のようにAとD、BとCをそれぞれ同じ数の組み合わせにすればOKです。
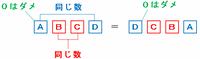
また、AとDには(1・1)から(9・9)までの9通りのうちのどれか、そしてBとCには(0・0)から(9・9)までの10通りのうちのどれかがあてはまるので、4けたの整数ABCDは全部で9×10=90通りできます。
また、AとDには(1・1)から(9・9)までの9通りのうちのどれか、そしてBとCには(0・0)から(9・9)までの10通りのうちのどれかがあてはまるので、4けたの整数ABCDは全部で9×10=90通りできます。
がんばってその90個の数(1001から9999まで)をたし算すれば答えは分かるのですが、それだと日が暮れてしまうので、合計の求め方をちょっと工夫してみましょう。
【その1 AとDの合計】
たとえば次の図のようにAとDに「1」をあてはめてみると、残りのBとCに入る数は(0・0)から(9・9)までの10通りが考えられるので、4けたの数「1BC1」は「1001」から「1991」までの10個になります。

同じように「2BC2」も10通り、「3BC3」も10通り、・・・と考えていくと、次の図のようにAとDには「1」から「9」までの数がそれぞれ10回ずつ使われることが分かります。
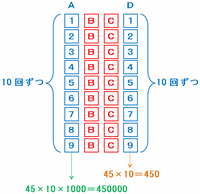
1から9までの和は45、そしてDには1から9がそれぞれ10回ずつ出てくるので、上の図のDに使われる数だけを縦にたし算すると45×10=450になります。
同じように「2BC2」も10通り、「3BC3」も10通り、・・・と考えていくと、次の図のようにAとDには「1」から「9」までの数がそれぞれ10回ずつ使われることが分かります。
1から9までの和は45、そしてDには1から9がそれぞれ10回ずつ出てくるので、上の図のDに使われる数だけを縦にたし算すると45×10=450になります。
Aに使われる数の合計も同じく450になるのですが、Aは千の位の数なので、その合計は450×1000=450000になります。
【その2 BとCの位の合計】
今度は次の図のようにBとCに「0」をあてはめてみると、残りのAとDに入る数は(1・1)から(9・9)までの9通りなので、4けたの数「A00D」は「1001」から「9009」までの9個になります。
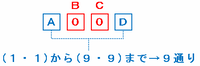
同じように「A11D」も9通り、「A22D」も9通り、・・・と考えていくと、次の図のようにBとCには「0」から「9」までの数がそれぞれ9回ずつ使われることになります。
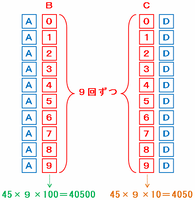
同じように「A11D」も9通り、「A22D」も9通り、・・・と考えていくと、次の図のようにBとCには「0」から「9」までの数がそれぞれ9回ずつ使われることになります。
0から9までの和は45、そしてBとCには0から9がそれぞれ9回ずつ出てきます。
Cは十の位の数なので、縦にたし算したときの合計は45×9×10=4050になります。
また、Bは百の位の数なので、その合計は45×9×100=40500になります。
以上から、Aの合計は450000、Bの合計は40500、Cの合計は4050、Dの合計は450になることが分かったので、ABCDの合計は450000+40500+4050+450=495000になります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
