いろいろな形の四角形が２００個あります。それらの四角形を辺や角の特徴によって個数を調べたところ、次のようになりました。
① ２組の向かい合った辺がそれぞれ平行な四角形→１２３個
② ４つの角がみな直角な四角形→４１個
③ ４つの辺の長さがみな等しい四角形→２８個
④ ②であり、③でもある四角形→ア個
⑤ ②ではなく、③でもない四角形→１４８個
次の問いに答えなさい。
(１)
アにあてはまる数はいくつですか。
(２)
平行四辺形ではあるが、ひし形でも長方形でもない四角形は何個ありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、四角形は辺の長さや内角の関係から「正方形・長方形・ひし形・平行四辺形・台形・その他の四角形」の６種類に分けられます。
なお、６種類目の「その他の四角形」とは、「長さの等しい辺や大きさの等しい角はなく、４本の辺がつながってるだけの図形」のことです。
※ 画像はクリックすると拡大します。
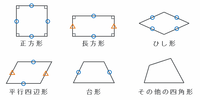
上の図の６種類が、問題文の①～⑤のどれにあてはまるのかを確認してみると、
① 正方形・長方形・ひし形・平行四辺形→１２３個
② 正方形・長方形→４１個
③ 正方形・ひし形→２８個
④ 正方形→ア個
⑤ 平行四辺形・台形・その他の四角形→１４８個
となるので、この問題で求めたいのは正方形の個数であることが分かります。
６種類の四角形が全部で２００個あり、⑤から「平行四辺形・台形・その他の四角形」の合計は１４８個あることも分かるので、「正方形・長方形・ひし形」の合計は２００－１４８＝５２個になります。
また、③から「正方形・ひし形」は合わせて２８個となることが分かるので、長方形は５２－２８＝２４個です。
②から「正方形・長方形」は合わせて４１個となることが分かるので、正方形は４１－２４＝１７個あります。
(２)
「平行四辺形ではあるが、ひし形でも長方形でもない四角形」とか言われるとなんだか難しく感じるかもしれませんが、さっきの図で６種類に分けた四角形の中で平行四辺形の数だけ答えればＯＫです。
※ ひし形と長方形は平行四辺形と特徴が似てるけど、それらは含めずに答えてね、という意味。
さっきの問題で「正方形・長方形・ひし形」の合計は５２個となることが分かりました。
また、①から「正方形・長方形・ひし形・平行四辺形」の合計は１２３個であることも分かるので、平行四辺形の数は１２３－５２＝７１個になります。
PR
