次の図の黄色い部分の面積は、一番大きな直角三角形の面積の何倍になるかを答えなさい。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずは次の図のように、この三角形の頂点や交点にＡ～Ｆの名前を付けておきます。
下の図の三角形ＡＢＣは、角ＢＡＣが３０度、角ＡＢＣが９０度なので、角ＡＣＢの大きさは１８０－(３０＋９０)＝６０度になります。
また、角ＦＣＢの大きさはもともと３０度であることが分かっているので、角ＥＣＦの大きさは６０－３０＝３０度になります。
※ 画像はすべて、クリックすると拡大します。
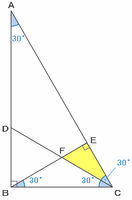
次は下の図の三角形ＣＥＦに注目してみると、角ＥＣＦは３０度、角ＦＥＣは９０度なので、角ＥＦＣの大きさは１８０－(３０＋９０)＝６０度になります。
また、三角形ＤＢＣは角ＦＣＢが３０度、角ＤＢＣが９０度なので、角ＢＤＣの大きさは１８０－(３０＋９０)＝６０度になります。
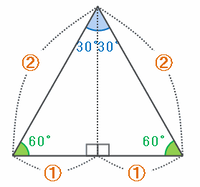
つまり、上の図の三角形ＡＢＣ、ＤＢＣ、ＥＦＣの３つは、どれも内角が３０度、６０度、９０度の直角三角形になっています。
そのような内角の直角三角形は、次の図のように正三角形を縦にスパッと切断してできる形なので、三角形の一番長い辺と一番短い辺の長さの比は２：１になります。
下の図の三角形ＥＢＣとＥＦＣは、３つの内角が３０度、６０度、９０度の直角三角形、そして三角形ＦＢＣは辺ＦＢ＝辺ＦＣの二等辺三角形になっています。
図の頂点Ｆから辺ＢＣに向けて赤い垂線ＦＧを引くと、角ＢＦＣは２等分されるので(１８０－６０)÷２＝６０度ずつになります。
また、点Ｇは辺ＢＣの真ん中になるので、辺ＢＧと辺ＧＣの長さはどちらも①と表せます。
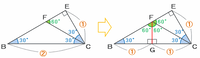
このとき、下の図の３つの三角形ＦＢＧ、ＦＧＣ、ＥＦＣは、
・どの三角形も３つの内角が３０度、６０度、９０度である
・２番目に長い辺の長さがどれも①である
となっているので、この３つの三角形は合同であることが分かります。
したがって、上の図の３つの三角形の面積をそれぞれ１とおくと、三角形ＥＢＣの面積は１×３＝３と表せます。
今度は下の図のように、三角形ＡＢＣとＢＥＣを並べて比べてみると、この２つの三角形はどちらも斜辺が底辺の２倍になっているので、辺ＥＣの長さを①とおくと辺ＢＣの長さは①×２＝②、そして辺ＡＣの長さは②×２＝④と表せます。
つまり、この２つの三角形は長さが２倍の相似になるので、三角形ＡＢＣの面積はＢＥＣの４倍になります。
※ 相似の図形は、長さの比が２倍なら面積比は２×２＝４倍。
さっき三角形ＥＦＣの面積を１とおくと三角形ＢＥＣの面積は３になることを確認したので、三角形ＡＢＣの面積は３×４＝１２と表せます。
以上から、黄色い部分(三角形ＥＦＣ)の面積は、一番大きい直角三角形であるＡＢＣの１÷１２＝１２分の１倍になります。
PR
