恵さんは、自転車でＡ町からＢ町に寄ってＣ町へ向かいます。Ａ町からは平らな道が続き、途中からＢ町までは４００ｍの上り坂です。また、Ｂ町からは平らな道が続き、途中からＣ町までは下り坂です。
午前１０時にＡ町を出発してから４分後に上り坂になり、さらに４分後にＢ町に着きました。ここで７分間休み、再びＢ町を出発したところ午前１０時３０分にＣ町に着きました。Ｂ町からＣ町までの距離は３６００ｍです。
自転車の速さは、平らな道では毎分２００ｍ、下り坂では毎分４００ｍです。このとき、次の問いに答えなさい。
(１)
上り坂での自転車の速さは毎分何ｍですか。
(２)
Ａ町からＢ町までの距離は何ｍですか。
(３)
恵さんがＡ町を出発してからＣ町に着くまでの様子を、Ａ町からの時間(分)と、Ａ町からの距離(ｍ)との関係のグラフに書き入れなさい。
※ 画像はクリックすると拡大します。
(４)
下り坂は何ｍですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
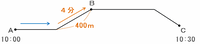
次の図のように、恵さんは上り坂の４００ｍを４分かけて進んだので、速さは４００÷４＝毎分１００ｍになります。
※ 画像はすべて、クリックすると拡大します。
(２)
恵さんは平地を分速２００ｍで進むので、次の図の青い矢印は２００×４＝８００ｍになります。
したがって、Ａ町からＢ町までの距離は８００＋４００＝１２００ｍになります。
(３)
Ａ町を１０時ちょうどに出発した恵さんはＢ町まで４×２＝８分かけて進み、そこで７分休けいするので、Ｂ町を出発する時刻は１０時１５分になります。
つまり、恵さんはＢ町からＣ町までの３６００ｍを、次の図のように３０－１５＝１５分かけて進むことが分かります。
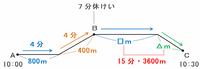
まずはＢＣ間の平地を進むのにかかった時間を求めるため、「もし１５分間すべて毎分４００ｍで進んだら」と仮定してつるかめ算を始めます。
もし１５分間ずっと毎分４００ｍで進むと、その距離は４００×１５＝６０００ｍになります。
実際のＢＣ間の距離は３６００ｍなので、つるかめ算の公式を利用して平地を進むのにかかった時間を求めると、(６０００－３６００)÷(４００－２００)＝１２分間になります。
つまり、恵さんはＢ町からの１２分間で平地を２００×１２＝２４００ｍ進み、残りの１５－１２＝３分間で下り坂を４００×３＝１２００ｍ進んでＣ町に到着しました。
ここまでの流れを振り返って、恵さんがＡ町からＣ町まで進んだときの様子をまとめてみると、
① Ａ町からの平地８００ｍを４分かけて進んだ
② 途中からの上り坂４００ｍを４分かけてＢ町まで進んだ(８分経過・合計距離１２００ｍ)
③ Ｂ町で７分休けいした(１５分経過・合計距離１２００ｍ)
④ Ｂ町からの平地２４００ｍを１２分かけて進んだ(２７分経過・合計距離３６００ｍ)
⑤ 途中からの下り坂１２００ｍを３分かけて進んだ(３０分経過・合計距離４８００ｍ)
となっているので、その様子をグラフに書きこむと次の図のようになります。
(４)
ＢＣ間の下り坂の距離は、さっきのつるかめ算で求めたように１２００ｍになります。
PR
