Ａ君がオートバイに乗って山に向かっています。山に向かってクラクションを鳴らすと１６秒後にこだまが聞こえてきました。それから１１秒後に再び鳴らすと、今度は１３秒後にこだまが聞こえてきました。音の速さを毎秒３４０ｍとすると、オートバイは山に向かって時速何㎞で走っていますか。
【補足】
これは入試問題ではなく、掲示板「インターエデュ」で取り上げられていたものです。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずは問題文の条件を３つの線分図に表し、最後にそれを重ね合わせて解いてみます。
【最初の１６秒のときの図】
次の図のように、オートバイはスタート地点から山に向かってクラクションを鳴らし、それからの１６秒間でオートバイは青色の矢印の分だけ、そして音は緑色の矢印の分だけそれぞれ進みました。
※ 画像はすべて、クリックすると拡大します。
【次の１１秒間の図】
次の図のように、オートバイはその後の１１秒間でさらに山へ向かって進み続けました。
ちなみにこの１１秒間は、オートバイはクラクションを鳴らさずに淡々と進んでいるだけです。
【最後の１３秒間の図】
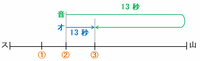
さっきの図で１１秒間進んだオートバイは、下の図の②の地点で再び山へ向かってクラクションを鳴らしました。
その後の１３秒間で、オートバイは青色の矢印の分だけ、そして音は緑色の矢印の分だけそれぞれ進みました。
【３つの線分図を並べてみる】
これまでの３つの線分図を次のように並べてみると、音が１６秒間で進んだときの矢印は、１３秒間で進んだときの矢印よりも下の図の「Ａ＋Ｂ＋Ｃ＋Ｄ(オレンジ色の部分)」だけ長いことが分かります。
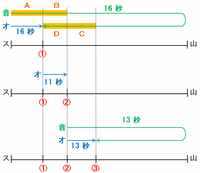
上の図のＡはオートバイが１６秒間で進む距離、ＢとＤはどちらもオートバイが１１秒間で進む距離、そしてＣはオートバイが１３秒間で進む距離なので、音が１６－１３＝３秒間で進む距離を、オートバイは１６＋１１＋１１＋１３＝５１秒間かけて進むことが分かります。
音が３秒間で進む距離は３４０×３＝１０２０ｍなので、オートバイの速さは１０２０÷５１＝秒速２０ｍになります。
最後にそれを３.６倍して時速に直すと、答えは２０×３.６＝時速７２㎞になります。
PR
