次の図のように、半径６㎝の円周上に４点Ａ、Ｂ、Ｃ、Ｄがあります。ＡＢとＣＤは長さが等しくて平行です。黄色い部分２か所の周の和が白い部分の周より、円周の長さの３分の２だけ長いとき、黄色い部分２か所の面積の和を求めなさい。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
黄色く塗られた２か所の周りの長さは、次の図の「青い孤ＡＢ＋ＣＤ」と「緑色の直線ＡＢ＋ＣＤ」に分けられます。
※ 画像はすべて、クリックすると拡大します。
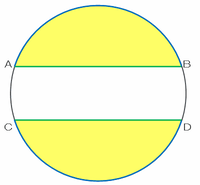
また、白い部分の周りの長さは、次の図の「赤い孤ＡＣ＋ＢＤ」と「緑色の直線ＡＢ＋ＣＤ」に分けられます。
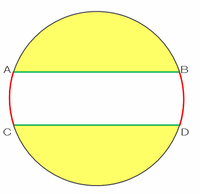
つまり、黄色い部分と白い部分の周りの長さには、どちらも「緑色の直線ＡＢ＋ＣＤ」が含まれているので、周りの長さの差は「青い孤ＡＢ＋ＣＤ」と「赤い孤ＡＣ＋ＢＤ」によって生じていることが分かります。
また、周りの長さの差は円周の３分の２にあたるので、円周の長さを１とおいて「青い孤ＡＢ＋ＣＤ」と「赤い孤ＡＣ＋ＢＤ」の長さの関係を次のような線分図に表すと、
・青い孤ＡＢ＋ＣＤの長さ→(１＋３分の２)÷２＝６分の５
・赤い孤ＡＣ＋ＢＤの長さ→１－６分の５＝６分の１
となることから、「青い孤ＡＢ＋ＣＤ」と「赤い孤ＡＣ＋ＢＤ」の長さの比は６分の５：６分の１＝５：１であることが分かります。
次の図の孤ＡＢと孤ＡＣの長さは５：１なので、おうぎ形ＯＡＢの中心角は１８０×６分の５＝１５０度、おうぎ形ＯＡＣの中心角は１８０×６分の１＝３０度になります。
※ １８０度を５：１に比例配分しました。
また、おうぎ形ＯＡＢの面積から二等辺三角形ＯＡＢの面積を引けば黄色く塗られた１か所の面積が分かるので、それを２倍すれば答えが求められます。
上の図のおうぎ形ＯＡＢは半径６㎝で中心角１５０度なので、その面積は６×６×３.１４×３６０分の１５０＝４７.１㎠です。
また、次の図の二等辺三角形ＯＡＢは、底辺をＯＢ＝６㎝とすると、高さはオレンジ色の直線ＡＥになります。
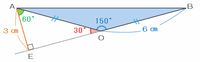
上の図の角ＡＯＥは３０度、角ＡＥＯは直角なので、角ＥＡＯの大きさは１８０－(３０＋９０)＝６０度です。
つまり、三角形ＡＥＯは３つの内角の組み合わせが「３０度・６０度・９０度」となるので、ちょうど正三角形を縦にスパッと二等分した形となり、辺ＡＥの長さはＯＡの長さの半分にあたる６÷２＝３㎝であることが分かります。
おうぎ形ＯＡＢの面積は４７.１㎠、そして二等辺三角形ＯＡＢの面積は６×３÷２＝９㎠なので、黄色く塗られた１か所の面積は４７.１－９＝３８.１㎠です。
したがって、黄色く塗られた２か所の面積の合計は３８.１×２＝７６.２㎠になります。
PR
