２種類の積み木アとイが合わせて４８個あり、その体積の合計は２２８０㎤です。アは立方体で、イは直方体です。アの体積の合計はイの体積の合計より１１９２㎤大きく、イのたて、横、高さは、アの１辺の長さの２１分の５倍、７分の１５倍、２５分の２８倍です。
(１) アの体積の合計は何㎤ですか。
(２) アは何個ありますか。また、アの体積は何㎤ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
アとイの体積の合計の関係を和差算の線分図に表すと次のようになるので、アの体積の合計は(２２８０＋１１９２)÷２＝１７３６㎤になります。
※ 画像はすべて、クリックすると拡大します。
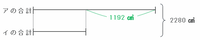
イの体積の合計も次の問題を解くのに必要なのでついでに求めておくと、２２８０－１１９２＝５４４㎤になります。
(２)
次の図のように、立方体アの１辺の長さを１とおくと、直方体イのたての長さは２１分の５、横の長さは７分の１５、そして高さは２５分の２８と表せます。
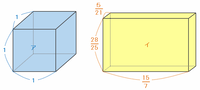
上の図の立方体アと直方体イの体積をそれぞれ求めてみると、
・立方体ア→１×１×１＝１
・直方体イ→２１分の５×７分の１５×２５分の２８＝７分の４
となることから、立方体アと直方体イの体積比は１：７分の４＝７：４であることが分かります。
立方体アと直方体イの体積の合計は、それぞれ「１個あたりの体積×立体の個数」を計算すれば求められるので、アの個数を□個、イの個数を△個とすると、
・立方体アの体積の合計→１個あたりの体積は７なので、７×□個＝１７３６㎤
・直方体イの体積の合計→１個あたりの体積は４なので、４×△個＝５４４㎤
と表すことができます(次の図参照)。
上の図から、立方体アの個数は１７３６÷７＝２４８、そして直方体イの個数は５４４÷４＝１３６となるので、アとイの個数の比は２４８：１３６＝３１：１７になります。
つまり、比の３１＋１７＝４８がアとイの個数の合計である４８個にあたるので、比の１は４８÷４８＝１個、そしてアの個数は１×３１＝３１個になります。
また、立方体アを３１個集めると体積の合計が１７３６㎤になるので、ア１個の体積は１７３６÷３１＝５６㎤です。
PR
