１辺が６㎝の正六角形ＡＢＣＤＥＦがあります。ＡＰ：ＰＦ＝２：１、ＡＲ：ＲＤ＝１：２、ＥＴ＝２㎝です。
※ 画像はクリックすると拡大します。
(１)
ＱＲの長さを求めなさい。
(２)
三角形ＡＱＰと四角形ＲＳＣＤの面積の比を、最も簡単な整数の比で表しなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
正六角形の１辺の長さは６㎝、そして辺ＡＰとＰＦの長さの比は２：１なので、辺ＡＰの長さは６×３分の２＝４㎝です。
また、次の図の辺ＡＤの長さはＦＥの２倍なので６×２＝１２㎝、そして辺ＡＲとＲＤの長さの比は１：２なので、辺ＡＲは１２×３分の１＝４㎝、辺ＲＤは１２×３分の２＝８㎝です。
※ 画像はクリックすると拡大します。
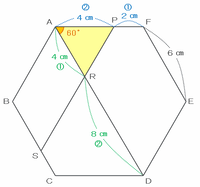
上の図の辺ＡＤは正六角形の内角ＢＡＰを２等分しているので、角ＰＡＲの大きさは１２０÷２＝６０度です。
つまり、三角形ＡＲＰは辺ＡＰとＡＲの長さがともに４㎝で角ＰＡＲが６０度なので、二等辺ではなく正三角形であることが分かります。
次の図の三角形ＡＲＰは正三角形なので、角ＡＲＰの大きさは６０度です。
また、辺ＤＡは正六角形の内角ＣＤＥを２等分しているので、角ＥＤＲの大きさも６０度です。
したがって、下の図の赤い直線ＰＳとＥＤは平行であることが分かります。
※ 角ＡＲＰと角ＲＤＥは同位角の関係にあり、その２つの角度が等しいから。
次の図の三角形ＡＲＱとＡＤＴの内角の関係を調べてみると、
・青い角ＲＡＱはどちらの三角形にも共通
・オレンジ色の角ＡＲＱとＲＤＴはどちらも６０度
・残った緑色の角ＡＱＲとＱＴＤの大きさも自動的に等しくなる
ことから、三角形ＡＲＱとＡＤＴは相似であることが分かります。
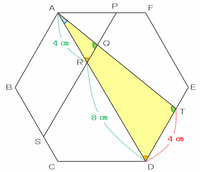
そこで、次の図のように三角形ＡＲＱとＡＤＴを並べて比べてみると、２つの三角形の底辺であるＡＲとＡＤの長さの比は４㎝：１２㎝＝１：３なので、辺ＱＲとＴＤの長さの比も１：３になっているはずです。
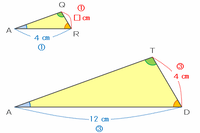
上の図のように、辺ＱＲの長さを□㎝とおくと、１：３＝□㎝：４㎝という比例式ができるので、辺ＱＲの長さは１×４÷３＝３分の４㎝になります。
(２)
次の図のように、辺ＰＳを左下へ伸ばし、辺ＣＤを左へ延長すると、六角形の左下に小さな正三角形ＳＵＣができます。
下の図の三角形ＲＵＤの１辺は８㎝、そして辺ＣＤは６㎝なので、正三角形ＳＵＣの１辺の長さは８－６＝２㎝であることが分かります。
また、正三角形ＡＲＰとＲＵＤは８の字相似の関係なので、ＡＲＰの高さを４とおくとＲＵＤの高さは８と表せます。
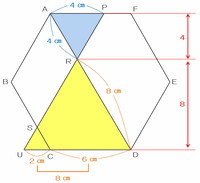
【三角形ＡＱＰの面積の割合を求める】
次の図の正三角形ＡＲＰの面積は４×４＝１６と表せます(÷２はすべての三角形で省略)。
また、辺ＲＰの長さは正三角形の１辺なので４㎝、辺ＱＲの長さは３分の４㎝なので、辺ＰＱの長さは４－３分の４＝３分の８㎝になります。
このとき、上の図の三角形ＡＲＱとＡＱＰは、底辺をそれぞれＱＲとＰＱと考えると高さが等しくなるので、この２つの三角形の面積比は底辺の比と同じく３分の４：３分の８＝１：２になります。
つまり、三角形ＡＱＰの面積は、三角形ＡＲＰの面積である１６を１：２に比例配分すれば求められるので、その割合は１６×３分の２＝３分の３２と表すことができます。
【四角形ＲＳＣＤの面積の割合を求める】
次の図の正三角形ＲＵＤの１辺は８㎝で高さが８なので、面積の割合は８×８＝６４と表せます。
また、左下の小さな正三角形ＳＵＣは１辺の長さが２㎝、そして高さは２と表すことができるので、面積の割合は２×２＝４となります。
四角形ＲＳＣＤの面積は、上の図の正三角形ＲＵＤからＳＵＣの面積を引けば求められるので、その割合は６４－４＝６０となります。
つまり、三角形ＡＱＰの面積の割合は３分の３２、四角形ＲＳＣＤの割合は６０と表せることが分かったので、三角形ＡＱＰと四角形ＲＳＣＤの面積比は、３分の３２：６０＝８：４５になります。
PR
