気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
10/27
Wed
2010
カリタス女子2010【4】 ☆場合の数・サイコロの目の出方☆
大、中、小3つのサイコロがあります。このとき、次の問いに答えなさい。
(1)
3つの目の和が8になるような目の出方は何通りありますか。
(2)
3つの目の数をかけると奇数になるような目の出方は何通りありますか。
(3)
3つの目の数をかけると偶数になるような目の出方は何通りありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(1)
3つの目の和が8になる組み合わせを、右へ行くほど数が大きくなるように書き出してみると、次の図のように(1・1・6)、(1・2・5)、(1・3・4)、(2・2・4)、(2・3・3)の5通りが考えられます。
※ 画像はすべて、クリックすると拡大します。
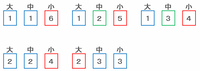
上の図の組み合わせを大きく2つのタイプに分けると、
・ 3つのうち2つの枠に同じ数をあてはめる「A・A・B」型
・ 3つの枠すべてに違う数をあてはめる「A・B・C」型
に分類できます。
このうち「A・A・B」型は、次の図のように3か所のどこにBをあてはめるのかを考えればOKなので、並べ替え方が3通りあります。

つまり、「A・A・B」型である(1・1・6)と(2・2・4)と(2・3・3)はそれぞれ並べ替え方が3通りずつあるので、合わせて3×3=9通りの組み合わせがあります。
つまり、「A・A・B」型である(1・1・6)と(2・2・4)と(2・3・3)はそれぞれ並べ替え方が3通りずつあるので、合わせて3×3=9通りの組み合わせがあります。
一方の「A・B・C」型の場合、次の図のように、
・ 大の枠→A・B・Cのうちどれか1つだから3通り
・ 中の枠→残り2つのうちのどちらかだから2通り
・ 小の枠→残った1つをあてはめるだけだから1通り
のように考えると、全部で3×2×1=6通りの並べ替え方があります。

つまり、「A・B・C」型である(1・2・5)と(1・3・4)はそれぞれ並べ替え方が6通りずつあるので、合わせて2×6=12通りの組み合わせがあります。
以上から、サイコロの目の出方は全部で9+12=21通りになります。
(2)
3つの数をかけた答えが奇数になるのは「奇数×奇数×奇数」のときだけなので、次の図のように大中小3つの目にはそれぞれ「1・3・5」のどれかがあてはまります。

つまり3つの枠がそれぞれ3通りずつなので、その組み合わせは全部で3×3×3=27通りになります。
(3)
3つの数のうちどれか1つが偶数なら、かけ合わせたときの答えも偶数になります。
ただ、それだと「奇数×奇数×偶数」とか「奇数×偶数×奇数」とか「偶数×奇数×偶数」とか「偶数×偶数×偶数」とか、とにかくいろんな場合がありすぎてやってられないので、「すべての組み合わせ」から「奇数になる場合」を引いて「偶数になる場合」が何通りなのかを求めます。
大中小3つのサイコロの目はそれぞれ1から6までの6通りなので、かけ算の答えの組み合わせは全部で6×6×6=216通りになります。
また、かけ算の答えが奇数になる場合の組み合わせはさっきの問題で27通りあることを確認しました。
したがって、かけ算の答えが偶数になる組み合わせは、全部で216-27=189通りになります。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
