整数には次のような性質があります。
【性質１】
それぞれの位の数の和が９の倍数となるとき、その整数は９の倍数である。
【性質２】
「右から奇数番目の位の数の和」と「右から偶数番目の位の数の和」の差が１１の倍数となるとき、その整数は１１の倍数となる。
このとき、次の各問いに答えなさい。
(１)
１１１１１１１１１は９９の倍数ですか。９９の倍数であれば○を、そうでなければ×を記入しなさい。
(２)
７けたの整数２６□△６０７について、□と△にあてはまる数の組を考えます。ただし、□と△には、０から９までの整数が入り、□は△より大きいとします。また、答えが□＝１、△＝０の組と□＝２、△＝１の組の場合、解答は(□・△)＝(１・０)、(２・１)と書くことにします。
① ２６□△６０７が９の倍数になるとき、□と△にあてはまる数の組をすべて答えなさい。
② ２６□△６０７が９９の倍数になるとき、□と△にあてはまる数の組をすべて答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
まずは問題文に書かれている「９の倍数」と「１１の倍数」の条件の意味を確認するため、７けたの整数「８３９０８４４」で実際に調べてみます。
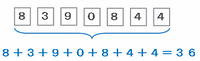
「８３９０８４４」に使われている７個の数の和を求めてみると、次の図のように３６になります。
このとき、３６は９の倍数なので、７けたの数「８３９０８４４」は９の倍数であることが分かります。
※ 画像はすべて、クリックすると拡大します。
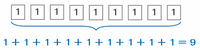
次は「８３９０８４４」の奇数番目の位と偶数番目の位にある数の和をそれぞれ求めてみると、
・奇数番目の位の和→８＋９＋８＋４＝２９
・偶数番目の位の和→３＋０＋４＝７
となります(下の図)。
このとき、２９－７＝２２は１１の倍数になっているので、７けたの数「８３９０８４４」は１１の倍数です。
つまり、「８３９０８４４」は９と１１の公倍数なので、９×１１＝９９の倍数であることが分かります。
【ここからが本題】
さっきの例と同じように、９けたの数「１１１１１１１１１」が９の倍数と１１の倍数の条件に合っているかどうかを調べてみます。
次の図のように、「１１１１１１１１１」の各位に使われている数の和を求めてみると９になります。
９はもちろん９の倍数なので、「１１１１１１１１１」は９の倍数であることが分かります。
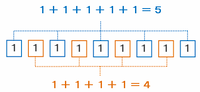
次は「１１１１１１１１１」の奇数番目の位と偶数番目の位にある数の和をそれぞれ求めてみると、
・奇数番目の位の和→１＋１＋１＋１＋１＝５
・偶数番目の位の和→１＋１＋１＋１＝４
となります(下の図)。
このとき、５と４の差である１はどう考えても１１の倍数ではないので、９けたの数「１１１１１１１１１」は１１の倍数ではありません。
つまり、「１１１１１１１１１」は９の倍数だけど１１の倍数ではないことが分かったので、９９の倍数ではありません。
したがって、解答らんには「×」と書き込みます。
(２)の①
７けたの数「２６□△６０７」に使われている各位の数の和を求めてみると、次の図のように「２１」と「□＋△」になります。
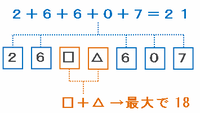
上の図の□と△にはそれぞれ０から９までの数字があてはまるので、「□＋△」の答えは最大で９＋９＝１８になります。
したがって、「２１」と「□＋△」との和を９の倍数にするには、「□＋△」の答えが２７－２１＝６の場合と３６－２１＝１５の場合の２通りが考えられます。
□は△よりも大きいことに気をつけながら、□＋△＝６と□＋△＝１５になる組み合わせを考えてみると、
・□＋△＝６になる場合→(□・△)＝(６・０)、(５・１)、(４・２)
・□＋△＝１５になる場合→(□・△)＝(９・６)、(８・７)
となるので、答えは(□・△)＝(６・０)、(５・１)、(４・２)、(９・６)、(８・７)の５組になります。
(２)の②
「２６□△６０７」が９の倍数と１１の倍数の条件を両方とも満たしていれば、９×１１＝９９の倍数であることが証明できます。
さっきの問題で□と△にいくつをあてはめれば９の倍数になるのかを確認したので、今度は１１の倍数にするための条件を確かめてみます。
まずは「２６□△６０７」の奇数番目の位と偶数番目の位にある数の和をそれぞれ求めてみると、
・奇数番目の位の和→２＋６＋７＋□＝１５＋□
・偶数番目の位の和→６＋０＋△＝６＋△
となります(下の図)。
この「１５＋□」と「６＋△」の差が１１の倍数であれば、「２６□△６０７」は１１の倍数になります。
□と△にはそれぞれ０から９があてはまるので、「１５＋□」の最大値は１５＋９＝２４、「６＋△」の最小値は６＋０＝６となります。
つまり、「１５＋□」と「６＋△」の差は最も大きい場合でも２４－６＝１８なので、この２つの数の差が１１の倍数になるのは、次の図のように「１５＋□」と「６＋△」の差が１１になるときしかありえません。
※ 次に大きい１１の倍数は１１×２＝２２。でもそれだと１８より大きいのでアウト。
ただ、この図だと□と△との関係がちょっと分かりにくいかもしれないので下の図のように書きかえてみると、□と△との差(図の緑色の部分)は１７－１５＝２であることが分かります。
さっきの問題で、(□・△)＝(６・０)、(５・１)、(４・２)、(９・６)、(８・７)の５組のとき、「２６□△６０７」は９の倍数になることが分かりました。
その５組の中で、□と△との差が２になるものを選べば「２６□△６０７」が１１の倍数の条件も満たすので、答えは(□・△)＝(４・２)になります。
PR
