気まぐれ解説カフェ(仮)
中学受験算数の入試問題を今日もゆるゆる解説中。算数プリントの無料ダウンロードは右横カテゴリ「プリントの無料ダウンロード」からどうぞ。
07/18
Mon
2011
愛知淑徳2011【4】 ☆公倍数・2つの数の最小公倍数の最大値と最小値を求める☆
2けたの数A、Bについて、Aは24の倍数で、Bは18の倍数です。AとBの最小公倍数は、最大で( ア )、最小で( イ )となります。ア、イにあてはまる数はいくつでしょう。
※ 続きを見る場合は、下の「解説はこちらから」をクリック!
(イ)の求め方
整数AとBはどちらも2けたの数なので、
・整数A→24、48、72、96のどれか
・整数B→18、36、54、72、90のどれか
になります。
また、それぞれの中で最小の数である24と18を素数の積で表してみると、次の図のように「24=2×2×2×3」、「18=2×3×3」となります。
※ 画像はすべて、クリックすると拡大します。

そもそも最小公倍数というのは「2つの数をそれぞれ□倍とか△倍して大きさをそろえた数のうち、最も小さい数」のことです。
上の図だと、24の中には「×2」が3個あるけど、18の中には「×2」が1個しかないので、次の図のように足りない2個分を18の方に追加してあげます。

上の図だと「×2」の数はどちらも3個ずつでそろったけど、「×3」の数は24の中には1個、18の中には2個のようにそろっていません。
そこで、次の図のように「×3」を24の方に1個追加すると、どちらの式も「2×2×2×3×3」となり、数がそろいます。
※ つまり、24と18の最小公倍数を求める式が完成しました。

以上から、整数AとBの最小公倍数のうち、最も小さい数は2×2×2×3×3=72となります。
【補足】
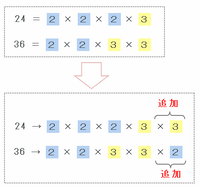
たとえば整数Aが24、そしてBが18ではなく36だったとしても、最小公倍数は次の図のように2×2×2×3×3=72となります。
・24を素数の積で表すと2×2×2×3。36を素数の積で表すと2×2×3×3。
・24は36に比べて「×3」が1個少ないので追加。
・36は24に比べて「×2」が1個少ないので追加。
・どちらの式も「2×2×2×3×3」でそろったので、それが最小公倍数となる。
(ア)の求め方
整数Aの条件にあてはまる数をそれぞれ素数の積で表してみると、
・24→2×2×2×3
・48→2×2×2×2×3
・72→2×2×2×3×3
・96→2×2×2×2×2×3
となります。
同じように、整数Bの条件にあてはまる数もそれぞれ素数の積で表してみると、
・18→2×3×3
・36→2×2×3×3
・54→2×3×3×3
・72→2×2×2×3×3
・90→2×3×3×5
となります。
それらの候補の中から、「自分は相手にない数をいっぱい持ってる」という組み合わせを選ぶと、数をそろえたときの最小公倍数が大きくなります。
たとえば、整数Aから「48→2×2×2×2×3」を、そして整数Bから「54→2×3×3×3」を選んでみると、
・48は54より「×2」が3個多いので、54に「×2」を3個追加。
・54は48より「×3」が2個多いので、48に「×3」を2個追加。
という流れで2つの数がそろい、どちらの式も「×2」が4個と「×3」が3個になるので、最小公倍数は2×2×2×2×3×3×3=432になります。
また、整数AとBから「72→2×2×2×3×3」という同じものを選んでしまうと、もうどちらの式にも追加できるものがないので、最小公倍数はそのまま72となります。
※ 「72と72の最小公倍数は72」という、非常に変な日本語です(笑)
「じゃあどの組み合わせなら、最小公倍数が最大になるの?」という本題に戻るわけですが、整数Bは「×2」が最も多くて3個しか使われてないので、整数Aから「96→2×2×2×2×2×3」を選べば、数をそろえたときに「×2」を5個使うことができます。
また、整数Aには「×5」がひとつもないので、整数Bから「90→2×3×3×5」を選べば、数をそろえたときに「×5」を1個使えます。
******** 補足 **************
整数Aは「×3」が最も多くて2個しか使われてないので、整数Bから「54→2×3×3×3」を選べば、数をそろえたときに「×3」を3個使う(つまり1個増やす)ことができます。
しかし、「×3」を1個増やすよりも「×5」を1個増やした方が、数をそろえたときの最小公倍数は大きくなるので、「54→2×3×3×3」は選べません。
******** 補足おしまい **************
というわけで、整数Aから「96→2×2×2×2×2×3」を、そして整数Bから「90→2×3×3×5」を選び、次の図のように数をそろえてみると、
・96は90より「×2」が4個多いので、90に「×2」を4個追加。
・90は96より「×3」が1個多いので、96に「×3」を1個追加。
・90は96より「×5」が1個多いので、96に「×5」を1個追加。
となります。
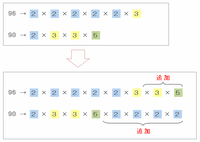
上の図から、96と90の最小公倍数は2×2×2×2×2×3×3×5=1440となるので、( ア )には1440があてはまります。
【追記】
結果的には「AとBから最小の数を選ぶ→最も小さい場合の最小公倍数が分かる」、「AとBから最大の数を選ぶ→最も大きい場合の最小公倍数が分かる」という非常に単純な流れになったので、「長々とややこしい説明だったけど全然意味ないよね」と思われること間違いなしです(笑)
でも、たとえばこの問題を「整数A→2けたとなる15の倍数」、「整数B→2けたとなる18の倍数」と置き換えてみると、必ずしも「最大のペア→最も大きい最小公倍数」とはならないことが分かります。
・2けたとなる15の倍数→15、30、45、60、75、90
・2けたとなる18の倍数→18、36、54、72、90
この場合、最大の数でペアを組むとどちらも90なので、最小公倍数は90です。
しかし、75と90なら最小公倍数が450になるので、「最大のペア→最も大きい最小公倍数」とは限らないことが分かります。
さらに、75と72なら最小公倍数が1800になる(このときが最大)ので、「大きい数の組み合わせを選べば、最小公倍数も大きくなる」なんて単純な話ではないことが分かります。
「じゃあ、こういう問題をどうやって解いたらいいの?」と振り出しに戻るわけですが、それは(イ)の求め方でも書いたように、
「自分は相手にない数をいっぱい持ってる」という組み合わせを選ぶと、数をそろえたときの最小公倍数が大きくなります。
という説明に尽きると思います。
PR
Comment
学校名で検索!
「フェリス」、「麻布」などの学校名を入力して検索すると該当記事の一覧が表示されます。 「該当なし」だったらごめんなさいm(_ _)m
カテゴリー
最新記事
(12/18)
(12/17)
(12/16)
(12/15)
(12/14)
(12/13)
(12/12)
(12/11)
(12/10)
(12/09)
(12/08)
(12/07)
(12/06)
(12/05)
(12/04)
(12/03)
(12/02)
(12/01)
(11/30)
(11/29)
リンク
最新コメント
プロフィール
HN:
ゆんたく
性別:
非公開
職業:
たびびと(Lv.4)
趣味:
チェロの演奏
自己紹介:
かつてゆんたくと呼ばれていたゆんたくです。
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
こんなゆんたくへ何か個人的に連絡したいことがおありでしたら、下記アドレスまでメールにてお願いいたします。
hassysar@gmail.com
