ある整数ａをｂ回かけた数の一の位の数を＜ａ・ｂ＞と書くことにします。たとえば、３×３×３×３＝８１なので＜３・４＞＝１となります。これについて、次の問いに答えなさい。
(１)
＜＜２・２＞・３＞を求めなさい。
(２)
ｘは１以上２０１１以下の整数とします。＜７・ｘ＞＝３となる整数ｘは何個ありますか。
(３)
ｙは１以上２０１１以下の整数とします。＜４・ｙ＞＋＜ｙ・４＞＝９となる整数ｙをすべて足し合わせるといくつになりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
＜２・２＞は２を２回かけた答えの一の位なので、２×２＝４です。
つまり、＜＜２・２＞・３＞＝＜４・３＞なので、次は４を３回かけ合わせてみると、４×４×４＝６４となります。
求めたいのはそのときの一の位の数なので、答えは４です。
(２)
＜７・ｘ＞＝３は「７をｘ回かけた答えの一の位が３となるとき」を表しています。
とりあえず、７を複数回かけ合わせた答えの一の位の規則性を調べてみると、次の図のように「７→９→３→１」の繰り返しであることが分かります。
※ 画像はすべて、クリックすると拡大します。
２０１１÷４＝５０２余り３なので、ｘに１から２０１１までの整数をあてはめたとき、答えの一の位は「７→９→３→１」が５０２回繰り返された後、「７→９→３」で終わります。
したがって、答えの一の位が３となる場合は全部で５０２＋１＝５０３回あります。
(３)
＜４・ｙ＞は「４をｙ回かけた答えの一の位」を表しているので、次の図のように４を複数回かけ合わせた答えの一の位の規則性を調べてみると、
・４を奇数回かけたとき→答えの一の位は４
・４を偶数回かけたとき→答えの一の位は６
となることが分かります。
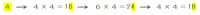
つまり、＜４・ｙ＞の答えは４または６のどちらかなので、
・＜４・ｙ＞＝４のとき→＜ｙ・４＞の答えは９－４＝５
・＜４・ｙ＞＝６のとき→＜ｙ・４＞の答えは９－６＝３
となります(次の図参照)。
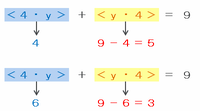
＜ｙ・４＞は「ｙを４回かけた答えの一の位」を表しているので、とりあえず「１×１×１×１」から「９×９×９×９」の答えの一の位を調べてみると、一の位が５となるときはあります(５×５×５×５のとき)が、３となるときはありません。
さっきの図で＜ｙ・４＞の答えは３と５のどちらかであることが分かっていたのですが、実際には＜ｙ・４＞＝３となることはあり得ないので、＜ｙ・４＞＝５であることが確定します。
※ ＜ｙ・４＞＝５のｙには５があてはまる。５を何回かけても答えの一の位は５。
つまり次の図のように、ｙには１から２０１１までの整数のうち、一の位に「５」がつく整数(たとえば５とか１５とか２３５とか１４７５とか) があてはまり、
・＜４・ｙ＞→４を奇数回かけることになるので、答えの一の位は必ず４
・＜ｙ・４＞→一の位に５がつく数を４回かけるので、答えの一の位は必ず５
となることから、＜４・ｙ＞＋＜ｙ・４＞＝４＋５＝９となります。
つまり次の図のように、ｙには「５→１５→２５→・・・→１９９５→２００５」のように、最小の５から１０ずつ増やして２００５まで進んだところまであてはまります。
(２００５－５)÷１０＝２００、２００＋１＝２０１個なので、ｙにあてはまる数は最小の５から最大の２００５まで２０１個あります。
※ 植木算の考え方。５と２００５は両端。２００は間の数。両端も含めるから個数は＋１。
以上から、ｙにあてはまるのは５から２００５までの一の位に５がつく２０１個の整数なので、その和は(５＋２００５)×２０１÷２＝２０２００５になります。
PR
