次の図の立方体において、点Ａから点Ｇへ辺を通って行く道すじを考えます。ただし、通った辺は戻らないこととします。
※ 画像はクリックすると拡大します。
(１)
３辺だけを通って行く道すじを考えます。辺ＡＢを通って行く場合( ① )通りあります。辺ＡＤを通って行く場合と辺ＡＥを通って行く場合も考えると、全部で( ② )通りあります。
(２)
５辺だけを通って行く道すじは、たとえばＡ→Ｂ→Ｃ→Ｄ→Ｈ→Ｇがあります。考えられる道すじをすべて書き出しなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)の①
辺ＡＢを通って点Ｇまで進む方法は、次の図のように
・Ａ→Ｂ→Ｃ→Ｇ
・Ａ→Ｂ→Ｆ→Ｇ
の２通りあります。
※ 画像はすべて、クリックすると拡大します。
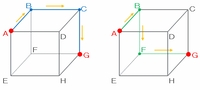
(１)の②
辺ＡＢを通って点Ｇへ行く方法が２通りなら、辺ＡＤ、辺ＡＥを通って点Ｇへ行く方法もそれぞれ２通りずつあるので、答えは全部で２×３＝６通りになります。
(２)
出発点であるＡから最初に行ける点はＢ、Ｄ、Ｅの３通りあるので、とりあえず辺ＡＢを使って５つの辺を通る方法を考えてみると、次の図のように
・Ａ→Ｂ→Ｃ→Ｄ→Ｈ→Ｇ
・Ａ→Ｂ→Ｆ→Ｅ→Ｈ→Ｇ
の２通りあります。
つまり、点Ａから最初にＤへ進んだ場合も、Ｇまで２通りの行き方があるはずなので探してみると、次の図のように
・Ａ→Ｄ→Ｃ→Ｂ→Ｆ→Ｇ
・Ａ→Ｄ→Ｈ→Ｅ→Ｆ→Ｇ
の進み方があります。
また、点Ａから最初にＥへ進んだ場合、Ｇまでの行き方は次の図のように
・Ａ→Ｅ→Ｆ→Ｂ→Ｃ→Ｇ
・Ａ→Ｅ→Ｈ→Ｄ→Ｃ→Ｇ
の２通りがあります。
以上から、答えは
・Ａ→Ｂ→Ｃ→Ｄ→Ｈ→Ｇ
・Ａ→Ｂ→Ｆ→Ｅ→Ｈ→Ｇ
・Ａ→Ｄ→Ｃ→Ｂ→Ｆ→Ｇ
・Ａ→Ｄ→Ｈ→Ｅ→Ｆ→Ｇ
・Ａ→Ｅ→Ｆ→Ｂ→Ｃ→Ｇ
・Ａ→Ｅ→Ｈ→Ｄ→Ｃ→Ｇ
になります。
PR
