１１、１２、１３の数字が書かれたカードが、それぞれ４枚ずつあります。この１２枚のカードを、Ａ君、Ｂ君、Ｃ君の３人に４枚ずつ配ります。持っている４枚のカードに書かれた数字の和を得点①とし、得点①の約数の個数を得点②とします。初めに配ったとき、得点①は全員同じで、Ｂ君のカードは４枚とも同じ数字でした。
(１)
３人のカードを１枚ずつ集めて配り直したところ、Ａ君とＢ君の得点②の差が７点でした。Ｃ君の得点②を求めなさい。
(２)
(１)の配り直されたカードを元に戻し、３人のカードを２枚ずつ集めて配り直したところ、３人の得点①がすべて異なり、得点②の最高点は４点でした。３人の得点①を小さい順に書きなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
１１、１２、１３と書かれたカードが４枚ずつあるので、その数字の合計は(１１＋１２＋１３)×４＝１４４になります。
得点①は全員同じだったので、３人に配られた４枚のカードの数字の和はそれぞれ１４４÷３＝４８ずつ、そしてＢ君は４枚のカードがすべて同じだったので、Ｂ君は４８÷４＝１２と書かれたカードを４枚もらったことが分かります。
※ いちいち計算するまでもなく、「３人のカードの合計が同じ」→「平均値も同じ」→「１１～１３の平均値は１２」→「３人のカードの平均値はそれぞれ１２」→「つまりＢは４枚とも１２」という流れで考えればＯＫです。
また、Ａ君とＣ君に配られたカードも、４枚の数字の合計はそれぞれ４８なので、２人はそれぞれ「１１」と「１３」を２枚ずつもらったことが分かります(次の図参照)。
※ 画像はすべて、クリックすると拡大します。
３人から１枚ずつカードを集めるとき、Ｂ君から回収されるのは間違いなく「１２」、その後に配り直されるのは「１１」、「１２」、「１３」のどれかなので、Ｂ君の４枚のカードの合計は
・「１１」が配られた場合→４８－１＝４７
・「１２」が配られた場合→４８のまま
・「１３」が配られた場合→４８＋１＝４９
の３パターンが考えられます。
また、Ａ君は「１１」または「１３」を回収され、その後に配り直されるのは「１１」、「１２」、「１３」のどれかなので、Ａ君の４枚のカードの合計は
・「１３」が回収されて「１１」が配られた場合→４８－２＝４６
・回収されたカードと配り直されたカードが同じ→４８のまま
・「１１」が回収されて「１３」が配られた場合→４８＋２＝５０
の３パターンが考えられます。
つまり、Ａ君およびＢ君の４枚のカードの合計として考えられる数字は４６から５０までの５種類なので、それぞれを素数の積で表してから約数の個数を求めてみると、
・４６→２×２３なので、約数の個数は(１＋１)×(１＋１)＝４個
・４７→素数なので、約数の個数は２個
・４８→２×２×２×２×３なので、約数の個数は(４＋１)×(１＋１)＝１０個
・４９→７×７なので、約数の個数は２＋１＝３個
・５０→２×５×５なので、約数の個数は(１＋１)×(２＋１)＝６個
となります(次の図参照)。
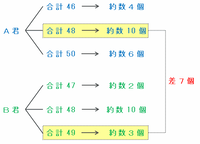
上の図から、Ａ君とＢ君の得点②(約数の個数の差)が７となるのは、
・Ａ君→回収されたカードと配り直されたカードが同じで、合計が４８のまま
・Ｂ君→「１２」が回収されて「１３」が配られ、合計が４８＋１＝４９になった
という場合しかありません。
また、すべてのカードに書かれた数字の合計は１４４なので、Ｃ君の４枚のカードに書かれた数字の合計は１４４－(４８＋４９)＝４７であることも分かります。
４７の約数の個数は２個なので、Ｃ君の得点②は２になります。
【補足】
「４６＝２×２３なので、約数の個数は(１＋１)×(１＋１)＝４個」とか「４８→２×２×２×２×３なので、約数の個数は(４＋１)×(１＋１)＝１０個」という計算の意味が分からん！という場合は、こちらのリンク先をサクッと流し読みしてみてください。
また、普通の整数は約数の個数が偶数なのに、Ａ君とＢ君の約数の個数の差が７(奇数)になったことから、２人のうちのどちらかは約数の個数が奇数のはずです。
約数の個数が奇数となるのは「３×３＝９」や「４×４＝１６」などのように、同じ数をかけ合わせた場合だけなので、Ｂ君は「７×７＝４９」に決定じゃん、という発想もＯＫだと思います。
(２)
３人のカードから２枚ずつ集めて配り直した後、３人のカードに書かれた数の合計は
・最小→「１１」が４枚そろった場合の１１×４＝４４
・最大→「１３」が４枚そろった場合の１３×４＝５２
となります。
また、約数の個数が４個となるのは「３×５＝１５」や「７×１１＝７７」などのように、２つの異なる素数をかけ合わせた場合だけなので、４４以上５２以下の整数でその条件にあてはまるものがあるか調べてみると、
・４６＝２×２３
・５１＝３×１７
の２パターンが考えられます。
たとえば、Ａの４枚のカードの合計が４６だった場合、ＢとＣのカードの合計は１４４－４６＝９８となります。
そして、Ｂの４枚のカードの合計が５２(考えられる合計の中の最大値)だったとすると、Ｃの合計は９８－５２＝４６となるのですが、それだとＡとＣの合計が同じになってしまうのでアウトです。
そこで、Ｂの４枚のカードの合計が５１
(考えられる合計の中で２番目に大きい数)だったとすると、Ｃの合計は９８－５１＝４７となるので３人の合計はバラバラであり、しかも次の図のように約数の個数が最大でも４個なのでＯＫです。
以上から、３人の得点①(４枚のカードに書かれた数字の合計)を小さい順に書き出すと、「４６・４７・５１」となります。
なお、解説では仮にＡ君を４６、Ｂ君を５１としたらＣ君は４７になりましたが、実際には誰がどの合計なのかなんてどうでもよくて、ただ単に解説の文章を分かりやすくするため適当に決めてみただけです。
PR
