２つの数の積について、Ａ～Ｅの５つの式が成り立ちます。このとき、★に入る数を求めなさい。ただし、同じ記号には同じ数が入ります。
Ａ：○×○＝２
Ｂ：△×△＝３
Ｃ：５×△＝□
Ｄ：☆×☆＝★
Ｅ：○×☆＝□－△
※ 解説を見る場合は、下の「解説はこちらから」をクリック！
ＡやＢの式を見て「同じ数をかけ合わせて２とか３になる数っていくつ？」なんて考え始めると、もうこの問題は解けません。
まずはＣとＥの式に注目しながら、その後でＤの式に視線を移していきます。
Ｃの式に「５×△＝□」とあることから、□は△５個分と等しいことが分かります。
つまり、Ｅの式の右辺にある「□－△」は、△５個から△１個を引く計算を表しているので、引き算の後には△が４個残ります。
したがって、Ｅの式は下の図のように「○×☆＝４×△」と書き換えることができます。
※ 画像はすべて、クリックすると拡大します。
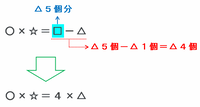
次はさっき変形したＥの式「○×☆＝４×△」の右辺にできた「４」に注目してみます。
Ａの式「○×○＝２」を利用して「４」を表すと、４＝２×２＝○×○×○×○となります。
したがって、Ｅの式の右辺にある「４」を「○×○×○×○」と入れ替え、ついでに左辺と右辺から「○」を１個ずつ取る(約分みたいな感じ)と、次の図のように「☆＝○×○×○×△」という式ができます。
次はＤの式「☆×☆＝★」の左辺にある２個の「☆」に、それぞれ「○×○×○×△」をあてはめてみると、「○×○×○×△×○×○×○×△＝★」という式ができます。
その式を次の図のようにもう少しスッキリさせてみると、左辺にはＡの式「○×○＝２」が３組とＢの式「△×△＝３」が１組できるので、「２×２×２×３＝★」という形になります。
以上から、★には２×２×２×３＝２４があてはまります。
PR
