(１) １２５より小さくて、１２５との最大公約数が１である整数は、何個ありますか。
(２) (１)で求めた整数をすべて足すといくつになりますか。
(３) ９８より小さくて、９８との最大公約数が１である整数をすべて足すと、いくつになりますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
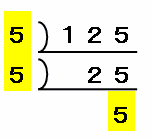
まずは１２５を素因数分解して素数の積で表してみると、次の図のように１２５＝５×５×５となるので、１２５は５で割れることが分かります。
※ 画像はすべて、クリックすると拡大します。
次にある数□と１２５の最大公約数を求めるときの連除法を次の図のように表してみると、□に５の倍数を入れると△には１ではなく５があてはまってしまうので、２つの数の最大公約数を１にするためには□に５の倍数以外の数をあてはめることになります。
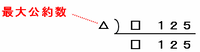
このとき、１から１２４の中にある５の倍数は、１２４÷５＝２４余り４なので２４個です。
その２４個以外の整数であれば１２５との最大公約数が１になるので、答えは全部で１２４－２４＝１００個になります。
(２)
大まかに言うと、
・１から１２４までの整数の和
・１から１２４の中にある５の倍数の和
の２つの差を求めればＯＫです。
１から１２４までの整数の和は、(１＋１２４)×１２４÷２＝７７５０になります。
また、１から１２４の中にある５の倍数は、５×１から５×２４＝１２０までの２４個なので、その和は(５＋１２０)×２４÷２＝１５００です。
したがって、答えは７７５０－１５００＝６２５０になります。
(３)
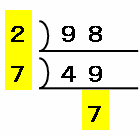
さっきと同じように、まずは９８を素因数分解して素数の積で表してみると、次の図のように２×７×７となるので、９８は２や７で割り切れます。
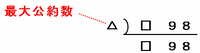
つまり、次の連除法の図の□に２や７の倍数以外をあてはめれば、２つの数の最大公約数が１になります。
そこでここからは、１～９７の中にある２や７の倍数をていねいに確かめていく作業に突入します。
大まかに言えば、さっきと同じように
① １から９７までの和を求める
② ２や７の倍数の和を求める
③ その２つの差を求めればＯＫ
という流れになります。
まずは１から９７までの和を求めてみると、(１＋９７)×９７÷２＝４７５３になります。
次に１から９７までの中にある２の倍数の和を求めてみると、１から９７の中には２×１＝２から２×４８＝９６までの４８個の２の倍数があるので、その和は(２＋９６)×４８÷２＝２３５２になります。
そして、次は１から９７の中にある７の倍数を数えていくのですが、「７×□」の□に偶数を入れたときの答えはすでに２の倍数としてさっき求めてしまったので、□に奇数をあてはめた場合のみ考えていきます。
「７×□」の□に奇数をあてはめ、その答えが９７以下にするためには、□に１から１３までの７個の奇数をあてはめればＯＫです。
７×１＝７、７×１３＝９１なので、その７個の和は(７＋９１)×７÷２＝３４３になります。
以上から、求める答えは４７５３－(２３５２＋３４３)＝２０５８になります。
PR
