３種類の数字が書いてあるカード「７」、「５」、「２」が合計１５枚あり、その数字の合計は７９でした。このような３種類のカードの組はいくつかあります。そのような枚数の組のうち「７」のカードの枚数が最大となるとき、それぞれの枚数を答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
７９÷７＝１１余り２なので、「７」のカードは最大で１１枚まで使え、そこへ次の図のように「２」のカードを１枚付け足してやれば合計がちょうど７９になります。
※ 画像はすべて、クリックすると拡大します。
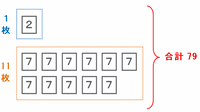
ただし、それだと「５」のカードを１枚も使っていないだけでなく、枚数の合計も１５枚になっていない(１１＋１＝１２枚)ので、問題文の条件に合っていません。
合計を７９のまま変えずにカードの枚数を増やすためには、「７」のカードを１枚減らし、その代わりに「２」と「５」のカードを１枚ずつ増やしていけばＯＫです。
その交換作業を１回行うたびにカードは１枚ずつ増えていくので、カードを１５－１２＝３枚増やすためには、次の図のように「７」のカード３枚を「２」と「５」のカード３組と入れ替えます。
上の図から、「７」は１１枚から３枚減ったので８枚、「５」は緑の枠の中にある３枚、そして「２」は青と緑の枠にある１＋３＝４枚になります。
PR
