式□×○×○＝２００があります。２つの□には同じ数字があてはまります。
(１)
□と○にあてはまる整数の組は何組ありますか。
(２)
(１)で求めた組の中で、□＋□＋○の値が最も小さい組をさがしなさい。そのときの□＋□＋○の値はいくらですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
とりあえず２００を素因数分解してみると次の図のようになるので、２００を素数の積で表すと「２×２×２×５×５」となります。
※ 画像はクリックすると拡大します。
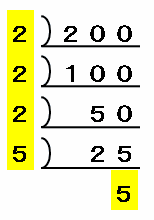
つまり、２００を整数の積で表すためには「２」を３回と「５」を２回かけ合わせる必要があるのですが、この問題は次の図のように３つのマス目しか用意されていないので、２か所の□に同じ数を入れた後の残りはすべてかけ合わせて１つの数字に直してから○にあてはめます。
例えば上の図の□に「２」を１つずつあてはめた場合、残りの数字は「２」「５」「５」なので、○には２×５×５＝５０があてはまります。
同じように□に「５」を１つずつあてはめてみると、残りの数字は「２」「２」「２」なので、○には２×２×２＝８があてはまります。
また、２か所の□にそれぞれ２×５＝１０をあてはめた場合、残りの数字である「２」はそのまま○にあてはめます。
したがって、組み合わせは全部で３組です、と言いたいところなのですが、よく考えてみれば１×１×２００でも条件にあてはまるので、答えは(２・５・５０)、(５・５・８)、(１０・１０・２)、(１・１・２００)の４組になります。
(２)
さっき見つけた４組の数の和をそれぞれ調べてみると次のようになります。
・(２・５・５０)→２＋５＋５０＝５７
・(５・５・８)→５＋５＋８＝１８
・(１０・１０・２)→１０＋１０＋２＝２２
・(１・１・２００)→１＋１＋２００＝２０２
したがって、３つの数の和がもっとも小さくなるのは(５・５・８)のときで、その和は１８になります。
PR
