Ａ＝１×２×３×４×・・・×９８×９９×１００とします。この数Ａを９で割り、その商を再び９で割るというように、割り切れなくなるまで９で割っていきます。このとき( )回割り算ができます。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
１００÷９＝１１余り１なので、１から１００の中には９の倍数が１１個あります。
したがって、９で１１回割り算ができます。おしまい。
・・・で正解なら話は早いのですが、現実はそんなに甘くないみたいです。
９＝３×３なので、まずは「１から１００の中に３が何個あるのか」を確認して、それを２で割ると「９が何個作れるのか」が分かります。
１から１００の中には、「３の倍数の仲間たち」が
・３が１個含まれている数→３の倍数(３、６、９、１２など)
・３が２個含まれている数→３×３＝９の倍数(９、１８、２７など)
・３が３個含まれている数→３×３×３＝２７の倍数(２７、５４、８１の３個)
・３が４個含まれている数→３×３×３×３＝８１の倍数(というか８１だけ)
の４種類あり、それらの関係をベン図に表すと次のようになります。
※ 画像はクリックすると拡大します。
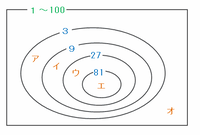
たとえば５４を素数の積で表してみると２×３×３×３となるので、５４の中には３が３個あります。
※ ５４は３の倍数、９の倍数、そして２７の倍数だから全部で３個。
そのうちの１個目は３の倍数として上の図のアに、２個目は９の倍数としてイに、そして３個目は２７の倍数としてウにあります。
そんな感じで、上のベン図のア～エにそれぞれ３が何個あるのかを確認してみると、
・ア(３の倍数)→１００÷３＝３３余り１だから３３個
・イ(９の倍数)→１００÷９＝１１余り１だから１１個
・ウ(２７の倍数)→１００÷２７＝３余り１９だから３個
・エ(８１の倍数)→８１しかないから１個
となるので、１から１００の中に、３は全部で３３＋１１＋３＋１＝４８個使われています。
それらを２個ずつ組み合わせると９ができるので、答えは４８÷２＝２４回になります。
※ ９が何個作れるのか＝９で何回割れるのか
PR
