Ａ先生とＢ先生は、健康のために毎週日曜日に、１周１㎞ある公園の周りを、同じ方向に、Ａ先生は歩き、Ｂ先生は走ります。ある日曜日、Ａ先生はトイレの前から歩き出しました。先に走っていたＢ先生は、Ａ先生が歩き出してから４分後にトイレの前を通過し、さらにその５分後、６７５ｍ先でＡ先生を追い抜きました。Ａ先生は６周して帰宅しました。その後Ｂ先生も帰宅しました。２人が同時に通過した場所のうちで、トイレに最も近い場所はトイレから何ｍ離れていますか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
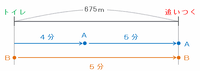
Ａがトイレを出発してから６７５ｍ先の地点でＢに追いつかれるまでの流れを次のような図に表してみると、Ａが６７５ｍを進むのにかかった時間は４＋５＝９分、Ｂが６７５ｍを進むのにかかった時間は５分なので、
・Ａの進む速さ→６７５÷９＝分速７５ｍ
・Ｂの進む速さ→６７５÷５＝分速１３５ｍ
となります。
※ 画像はすべて、クリックすると拡大します。
また、ＢがＡに追いついたのはトイレから右回りに６７５ｍ進んだ地点ですが、このコースは１周１㎞＝１０００ｍなので、トイレとの距離は次の図のように１０００－６７５＝３２５ｍと考えられます。
※ 左回り・右回りのうち、トイレまでの距離が近い方を採用する。
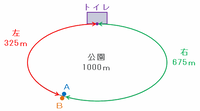
上の図の状態から、ＢはＡに１０００÷(１３５－７５)＝３分の５０分ごとに追いつくので、その間にＡは７５×３分の５０＝１２５０ｍずつ進みます。
つまり、追いつく地点は上の図から１２５０ｍずつ先へずれていくので、たとえば２回目に追いつく地点は、６７５＋１２５０＝１９２５ｍ、１９２５－１０００＝９２５ｍとなることから、次の図のようにトイレから右へ９２５ｍ、左へ１０００－９２５＝７５ｍの地点です。
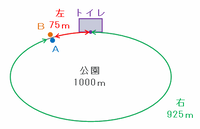
そんな感じで、Ａが帰るまでに進んだ６周＝６０００ｍを超えるまでの追いつき地点を確認してみると、
・３回目→１９２５＋１２５０＝３１７５ｍ、３１７５－３０００＝１７５ｍなので、トイレから右へ１７５ｍ
・４回目→３１７５＋１２５０＝４４２５ｍ、４４２５－４０００＝４２５ｍなので、トイレから右へ４２５ｍ
・５回目→４４２５＋１２５０＝５６７５ｍ、５６７５－５０００＝６７５ｍなので、トイレから右へ６７５ｍ、左へ１０００－６７５＝３２５ｍ
となります(次は６０００ｍを超えるのでアウト)。
以上から、追いつき地点の中でトイレに最も近いのは、トイレから左へ７５ｍのとき(２回目の追いつき)です。
PR
