１から５０までの整数をすべてかけ合わせた数をＡとします。次の図の計算のようにＡを「３、５、７、９、３、５、７、９、・・・」の順に繰り返し割っていくとき、初めて割り切れなくなるのは３、５、７、９のうち、どれで割ったときですか。
※ 画像はクリックすると拡大します。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
１から５０までをかけ合わせてできた整数Ａを３、５、７、９で１回ずつ割るとき、
・３で１回割る→Ａの中にある３が１個消える
・５で１回割る→Ａの中にある５が１個消える
・７で１回割る→Ａの中にある７が１個消える
・９で１回割る→９＝３×３なので、Ａの中にある３が２個消える
となることから、「３→５→７→９」の順に１回ずつ割ると、Ａから３が１＋２＝３個、５と７が１個ずつ消えます(消える＝約分みたいなイメージ)。
※ 画像はすべて、クリックすると拡大します。
１～５０をかけ合わせた整数Ａの中には、「３の倍数」、「３×３＝９の倍数」、「３×３×３＝２７の倍数」という３種類の「３の倍数グループ」があり、
・５０÷３＝１６余り２なので、下の図のアは１６個
・５０÷９＝５余り５なので、下の図のイは５個
・５０÷２７＝１余り２３なので、下の図のウは１個
となることから、１～５０をかけ合わせた整数Ａの中には、３が全部で１６＋５＋１＝２２個含まれています。
********* ちょっと補足 **********************************
たとえば１８を素数の積で表すと「２×３×３」となるので、１８には３が２個含まれています。
そのうちの１個目は「３の倍数」として上の図のアにあてはまり、２個目は「９の倍数」として上の図のイにあてはまります。
********* 補足おしまい **********************************
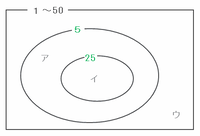
また、１～５０をかけ合わせた整数Ａの中には、「５の倍数」、「５×５＝２５の倍数」という２種類の「５の倍数グループ」があり、
・５０÷５＝１０なので、下の図のアは１０個
・５０÷２５＝２なので、下の図のイは２個
となることから、１～５０をかけ合わせた整数Ａの中には、５が全部で１０＋２＝１２個含まれています。
そして、１～５０をかけ合わせた整数Ａの中には、「７の倍数」、「７×７＝４９の倍数」という２種類の「７の倍数グループ」があり、
・５０÷７＝７余り１なので、下の図のアは７個
・５０÷４９＝１余り４９なので、下の図のイは１個
となることから、１～５０をかけ合わせた整数Ａの中には、７が全部で７＋１＝８個含まれています。
つまり次の図のように、１～５０をかけ合わせた整数Ａの中には、３が２２個、５が１２個、そして７が８個含まれています。
そして、それらの在庫は整数Ａを「３→５→７→９」の順に１回ずつ割るごとに、３が１＋２＝３個、５と７が１個ずつ消えていきます。
とりあえず、整数Ａを「３→５→７→９」の順に７回割ってみると、
・３→３×７＝２１個使うので、残りは２２－２１＝１個
・５→７個使うので、残りは１２－７＝５個
・７→７個使うので、残りは８－７＝１個
となるので、次の図のように３と７の在庫がギリギリまで減ってしまいます。
再び「３→５→７」の順に割った時点で、上の図の「３」と「７」の在庫はついになくなるので、次に９で割ることはできません。
以上から、答えは９で、それは整数Ａを「３→５→７→９」の順に割った８回目のときです。
PR
