ある運動会で６チームが特典を争い、得点の高い順に１位から６位まで順位を決めた結果、その得点は次のようになりました。
・６チームの合計得点は７５００点でした。
・１位と２位、２位と３位、３位と４位、４位と５位、５位と６位の得点の差がすべて同じでした。
・２位と３位の得点の合計と、１位と４位と５位と６位の得点の合計の比は２：３でした。
このとき、次の各問いに答えなさい。
(１) 各順位の得点の差を求めなさい。
(２) ６位の得点を求めなさい。
(３) １位の得点を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
６位のチームの得点を□点、各チーム間の得点差を①とおくと、１位から６位までの各チームの得点は次のような線分図に表すことができます。
たとえば、５位のチームの得点は６位よりも①だけ多いので「□点＋①」、４位のチームはそれよりもさらに①だけ多いので「□点＋②」といった感じです。
※ 画像はすべて、クリックすると拡大します。
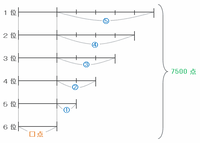
上の図を参考にして「２位と３位の得点の合計」と「１位と４位と５位と６位の得点の合計」をそれぞれ求めてみると、
・２位と３位→(□点＋④)＋(□点＋③)＝□点×２＋⑦
・１位と４位と５位と６位→(□点＋⑤)＋(□点＋②)＋(□点＋①)＋□点＝□点×４＋⑧
となります。
また、６チームの合計である７５００点を２：３に比例配分すれば「２位と３位の得点の合計」と「１位と４位と５位と６位の得点の合計」がそれぞれ分かるので、
・２位と３位→７５００×５分の２＝３０００点
・１位と４位と５位と６位→７５００×５分の３＝４５００点
となることから、「□点×２＋⑦＝３０００点」と「□点×４＋⑧＝４５００点」という２つの式ができます。
「□点×２＋⑦＝３０００点」の式全体を２倍にすると「□点×４＋⑭＝６０００点」となるので、その式と「□点×４＋⑧＝４５００点」を次の図のように並べて消去算っぽく比べてみると、⑭－⑧＝⑥が６０００－４５００＝１５００点にあたることが分かります。
求めたいのは各順位の得点差(つまり比の①)なので、答えは１５００÷⑥＝２５０点になります。
(２)
次の図の比の①が２５０点なので、比の①＋②＋③＋④＋⑤＝⑮は、２５０×⑮＝３７５０点です。
※ 下の図の青い部分の合計が３７５０点。
つまり、上の図から青い部分をすべて取り、全チームを６位の点数にそろえると７５００－３７５０＝３７５０点になるので、６位の得点は３７５０÷６＝６２５点です。
(３)
１位の得点は、６位の得点よりも比の⑤だけ多いので、６２５＋２５０×⑤＝１８７５点です。
PR
