５４０㎞離れたＡ地点からＢ地点まで、高速道路を利用して車で移動しました。車は１リットルのガソリンで１２㎞走ることができます。車は時速８０㎞で走り、途中、３０分の休憩を２回とりました。次のグラフは、車がＡ地点を９時に出発してからの時間と車に残っているガソリンの量の関係を表したものです。
※ 画像はクリックすると拡大します。
(１)
はじめに休憩をとったとき、車に残っていたガソリンは何リットルですか。
(２)
途中、ガソリンを入れたのは何時何分ですか。
(３)
Ｂ地点に着いたとき、車に残っていたガソリンは何リットルですか。
(４)
Ｂ地点に着いたのは、何時何分ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次のグラフの青い部分は、９時から１０時３０分までの１.５時間を表しています。
その間に車は時速８０㎞で進み続けるので、走行距離は８０×１.５＝１２０㎞になります。
※ 画像はすべて、クリックすると拡大します。
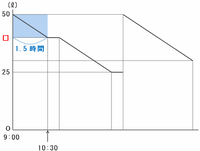
車は１２㎞進むごとにガソリンを１リットルずつ消費するので、１２０㎞走った場合は１２０÷１２＝１０リットルのガソリンが必要になります。
したがって、最初に休憩をとったときのガソリンの残量(上のグラフの赤い□)は、５０－１０＝４０リットルになります。
(２)
１０時３０分に最初の休憩地点へ到着した車は、次のグラフのように３０分休憩してから次の休憩地点に向けて１１時ちょうどに出発し、ガソリンを４０－２５＝１５リットル使って走行しました。
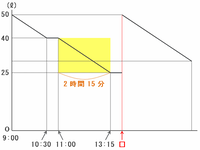
ガソリン１５リットル分の走行距離は１２×１５＝１８０㎞、その距離を時速８０㎞で進むのにかかる時間は１８０÷８０＝２.２５時間＝２時間１５分なので、車が次の休憩地点に到着した時刻は１１時＋２時間１５分＝１３時１５分です。
ただし、ガソリンを入れたのは上のグラフの赤い点線の部分(２回目の休憩を終えたとき)なので、答えは１３時１５分＋３０分＝１３時４５分になります。
(３)
次のグラフの青い部分の走行距離は１２０㎞、黄色い部分の走行距離は１８０㎞なので、１３時４５分に休憩地点を出発するとき、Ｂ地点までの残りは５４０－(１２０＋１８０)＝２４０㎞になっています。
２４０㎞を走行するのに必要なガソリンの量は２４０÷１２＝２０リットルなので、Ｂ地点に着いたときのガソリンの残量(上のグラフの赤い□)は５０－２０＝３０リットルになります。
(４)
次のグラフのように、車は１３時４５分に２回目の休憩を終えて、Ｂ地点までの２４０㎞を走行します。
この車は２４０㎞を進むのに２４０÷８０＝３時間かかるので、Ｂ地点に到着したときの時刻は１３時４５分＋３時間＝１６時間４５分になります。
PR
