時針(短針)と秒針がそれぞれ一定の速さで回転し、正しい時間でちょうど１分ごとに重なる時計があります。この時計の時針と秒針の回転の向きは正しい時計と同じで、時針と秒針の回転する速さの比も正しい時計と同じです。この時計の１時間は、正しい時間で( )分( )秒です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
普通の時計の場合、１２時ちょうどのときは次の図のように秒針と短針がどちらも「１２」の目盛りを指していますが、その１時間後には秒針が「１２」の目盛りを、そして短針は「１」の目盛りを指しています。
※ 画像はクリックすると拡大します。
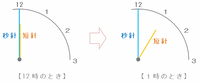
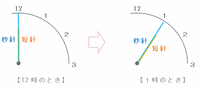
しかしこの時計は、１分ごとに秒針と短針が重なっているので、１２時ちょうどのときも１時ちょうどのときも２つの針は次の図のように重なっています。
つまり次の図のように、このニセ時計は１２時ちょうどから１時ちょうどまでの１時間で秒針が５秒分だけ先へ進んだので、ニセ時計の１時間は、実際の時間だとそれよりも５秒前にあたる５９分５５秒になります。
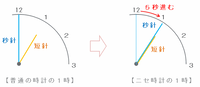
【補足】
普通の時計なら、秒針が時計盤を３６０度進む間に短針も０.５度進むので、１分ごとに秒針と短針が重なることはあり得ません。
もしニセ時計の短針だけが普通の時計の短針と同じ速さで進むのであれば、秒針が１分間に３６０.５度進めば１分ごとに２つの針が重なります。
ただし、このニセ時計の秒針と短針には「秒針と短針の回転する速さの比は、正しい時計の秒針と短針が回転する速さの比と同じ」という条件があるので、秒針の進む速さが普通の時計よりもちょっとだけ速いのなら、短針の進む速さも同じ割合でちょっとだけ速くなっているはずです。
※ 秒針の進む速さが普通の時計の１.１倍なら、短針の進む速さも同じく１.１倍。秒針の進む速さが普通の時計の１.２倍なら、短針の進む速さも同じく１.２倍。・・・みたいな感じ。
つまり、このニセ時計の針はどちらも普通の時計よりちょっとだけ進みが速いので、もし１２時に２つの針を「１２」の目盛りに合わせると、１時間後には２つの針が「１」よりもほんの少しだけ進んだところで重なることになります。
PR
