次の図の【例】のように、計算式□□÷□＋□÷□□の６か所の空欄に、１、２、３、４、５、６、７、８、９の９個の数字から６個を入れて、計算します。ただし、同じ数字を２か所以上で用いてはいけません。
※ 画像はクリックすると拡大します。
(１) 計算結果が最も大きな整数となるような数字の入れ方を答えなさい。
(２) 計算結果が２５となるような数字の入れ方をすべて答えなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図の「ＡＢ÷Ｃ」の答えを最大にするには「９８÷１＝９８」とすればＯＫなのですが、その場合、青い部分の答えが９８÷２＝４９と整数になるため、緑色の「Ｄ÷ＥＦ」の答えも整数にしないと、計算結果が整数になりません。
※ 画像はすべて、クリックすると拡大します。
しかし、上の図のＤは１けた、ＥＦは２けたの数なので、「Ｄ÷ＥＦ」の答えが整数となることは絶対にありえません。
※ 「小さい数÷大きい数」の答えは１未満なので、整数になるわけがない。
また、「ＡＢ÷Ｃ」を「９８÷２」としても答えが４９で整数となりダメなので、次の図のように「ＡＢ÷Ｃ」を「９７÷２」にしてみると、青い部分の答えは９７÷２＝４８.５になります。
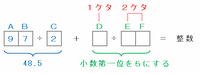
つまり、上の図の「Ｄ÷ＥＦ」の答えの小数第一位が「５」になれば、計算結果が整数になるので、残りの数「１・３・４・５・６・８」を使ってＤがＥＦの２分の１となる組み合わせを探してみると、「８÷１６」のときしかないことが分かります。
※ ＤがＥＦの２分の１なら、Ｄ÷ＥＦ＝２分の１＝０.５となり、小数第一位に「５」が出てくる。
以上から、計算結果がもっとも大きな整数となる式は、９７÷２＋８÷１６となります。
(２)
さっきの問題で、
・「ＡＢ÷Ｃ」の答えを整数にすると、計算結果が整数にはならない。
・「Ｄ÷ＥＦ」の答えは１未満の小数または分数となる。
ことが分かったので、その２つのことを頭の片隅に置きながら問題を解いていきます。
計算結果の２５を分数で表すと、１分の２５、２分の５０、３分の７５、４分の１００、・・・のようにはてしなく作ることができます。
たとえば「ＡＢ÷Ｃ」の答えを１分の２５にもっとも近い１分の２４にするため、次の図のように「ＡＢ÷Ｃ＝２４÷１」にしてみると、計算結果を２５にするためには「Ｄ÷ＥＦ」の答えを２５－２４＝１にしなければなりません。
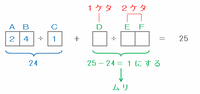
ところが、「Ｄ÷ＥＦ」の答えは必ず１未満なので、上の図の計算結果が２５となることはありません。
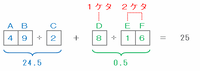
そこで、今度は「ＡＢ÷Ｃ」の答えを２分の５０にもっとも近くするため、「ＡＢ÷Ｃ＝４９÷２」にしてみると、
・「ＡＢ÷Ｃ」の答えは４９÷２＝２４.５
・「Ｄ÷ＥＦ」の答えは２５－２４.５＝０.５
なので、次の図のように「Ｄ÷ＥＦ」を８÷１６にすればＯＫです。
※ Ｃ＝２なので、「６÷１２」はダメ。Ａ＝４なので、「７÷１４」もダメ。
また、「ＡＢ÷Ｃ」の答えを３分の７５にもっとも近くするため、「ＡＢ÷Ｃ＝７４÷３」にしてみると、
・「ＡＢ÷Ｃ」の答えは７４÷３＝３分の７４
・「Ｄ÷ＥＦ」の答えは３分の７５－３分の７４＝３分の１
なので、次の図のように「Ｄ÷ＥＦ」を６÷１８にすればＯＫです。
※ Ｂ＝４なので、「４÷１２」はダメ。「５÷１５」はＤとＦが同じ数になるのでダメ。
「ＡＢ÷Ｃ」の答えを４分の１００にもっとも近くするには、「ＡＢ÷Ｃ＝９９÷４」としたいのですが、それだとＡとＢが同じ数になってしまうのでアウトです。
そこで、今度は「ＡＢ÷Ｃ」の答えを２分の５０にもっとも近くするため、「ＡＢ÷Ｃ＝９８÷４」にしてみると、
・「ＡＢ÷Ｃ」の答えは９８÷４＝２４.５
・「Ｄ÷ＥＦ」の答えは２５－２４.５＝０.５
なので、次の図のように「Ｄ÷ＥＦ」を６÷１２にすればＯＫです。
※ Ｂ＝８なので、「８÷１６」はダメ。Ｃ＝４なので、「７÷１４」もダメ。
「ＡＢ÷Ｃ」の答えを５分の１２５にもっとも近くするには、「ＡＢ÷Ｃ＝１２４÷５」としたいのですが、ＡＢに３ケタの数をあてはめることはできません。
そこで、「ＡＢ÷Ｃ＝９８÷５」にしてみると、
・「ＡＢ÷Ｃ」の答えは９８÷５＝５分の９８
・「Ｄ÷ＥＦ」の答えは５分の１２５－５分の９８＝５分の２７
となるのですが、「Ｄ÷ＥＦ」の答えが仮分数になることはあり得ないので式が作れません。
以上から、計算結果が２５となる式は、「４９÷２＋８÷１６」、「７４÷３＋６÷１８」、「９８÷４＋６÷１２」の３通りになります。
PR
