次の図１のように、１辺の長さが１㎝の正方形のマスがたてに２個、横に２０１１個、合計４０２２個ならべて書いてあります。左上のマス目をＡ、右上のマス目をＢ、右下のマス目をＣとします。
※ 画像はすべて、クリックすると拡大します。
図２のように、上の目の数が１になるようにサイコロをマス目Ａの上におきます。このサイコロをマス目Ａからマス目Ｃまで、辺をじくにして、たおしていきます。そのとき、最初にマス目Ａにあるサイコロの上の目の数１と、サイコロをたおすたびにサイコロの上にあらわれる数を記録します。サイコロがマス目Ｃについたときに記録した数を合計し、その合計をＴとします。ただし、サイコロは、向かい合う面に書かれている数の和が７となるように作られています。サイコロはこのマス目の外には出ないものとして、次の各問いに答えなさい。
(１)
サイコロをたおしながら、マス目Ａからマス目Ｂまでまっすぐ転がしたのち、マス目Ｃへ１回たおすとき、Ｔはいくつになりますか。
(２)
マス目Ａからマス目Ｃまでもっとも少ない回数でサイコロをたおしながら転がします。Ｔがもっとも小さくなるとき、Ｔはいくつになりますか。また、そのような転がし方は何通りありますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
次の図のように、最初は「１」の面が上にある状態のサイコロを右へ倒していくと、真上に来る面は「１→４→６→３」の繰り返しになります。
※ 画像はすべて、クリックすると拡大します。
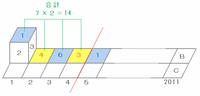
２０１１÷４＝５０２余り３なので、「１→４→６→３」を５０２回繰り返した後、次の図のように真上の面が「１→４→６」と変わったときに右端のＢのマスへ到着します。
また、最後にサイコロを手前にころりん！と倒してＣのマスへ到着したとき、真上の面は「２」の反対側の「５」になっています。
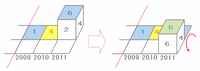
(１＋４＋６＋３)×５０２＝７０２８、１＋４＋６＝１１、そして最後に真上に来た「５」も含めると、答えは７０２８＋１１＋５＝７０４４になります。
(２)
次の図のように、サイコロを最初の位置から２００８番目のマスまでひたすら右に転がしている間は、真上に来る目が「１→４→６→３」の繰り返しになります。
２００８÷４＝５０２組目までの数字の合計が(１＋４＋６＋３)×５０２＝７０２８となるところまではさっきの問題と変わらないので、残り３マスのどこでサイコロを手前に転がせば合計が最も小さくなるのかを考えてみます。
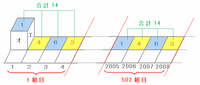
次の左側の図のように、サイコロを右へ「１→４→６」と進めてから手前に転がすと、最後の目は「５」になるので、そのときの４つの数の合計は１＋４＋６＋５＝１６になります。
また、右側の図のようにサイコロを右へ「１→４」と進めてから手前に転がして「５」の目を出し、最後にもう１回右へ転がすと最後が「６」になるので、そのときの４つの数の合計は１＋４＋５＋６＝１６です。
※ つまり、下の図だとどちらもさっきの問題のときと合計が変わらない。
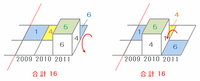
しかし次の図のように「１」のときにサイコロを手前に倒し、その後で右へ２回転がすと、４つの数の合計は１＋５＋４＋２＝１２となり、さっきの図に比べて合計が１６－１２＝４減ります。
また、次の図のように２００８番目のマスでサイコロを手前に倒し、その後で右へ３回転がしてもＯＫなのですが、その場合の４つの数の合計は５＋１＋２＋６＝１４なので最小ではありません。
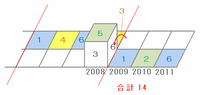
以上から、最小となるＴの値は７０２８＋１２＝７０４０となります。また、さっきの問題のときはＴの値が７０４４で、最小となる場合はそれよりも１６－１２＝４小さいので、７０４４－４＝７０４０と求めてももちろんＯＫです。
また、Ｔの値を最小にするには、真上の面が「１」となったときにサイコロを手前に倒せばＯＫなので、そのタイミングは
・サイコロが右へ「１→４→６→３」と５０２回繰り返しながら転がす途中
・最後の「１→４→６」のときの「１」
のどこか１回を選ぶことになります。
したがって、Ｔの値を最小にする転がし方は、全部で５０２＋１＝５０３通りになります。
【補足】
次の図のように、途中の「１」でサイコロを手前に倒した場合、真上の面が「５」になってから最初の３つは「５→４→２」となった後、そこからは「３→５→４→２」の繰り返しになります。
最初にどの面が上だったとしても、ひたすら右へ転がし続ける限りは４つの面の合計が７×２＝１４になることは変わらないので、途中で１回だけサイコロを手前に倒して「１→５→４→２」を作ればＴの値が最小になります。
PR
