次の図のように、ある山に分速４５ｍで時計回りに動くリフトがあります。このリフトのケーブルは長方形の形になっており、その長方形の横の長さは５ｍです。このケーブルには１人乗りの座席が等間隔についており、座席には反時計回りで１番から順番に１２３番まで番号がついています。
※ 画像はすべて、クリックすると拡大します。
今、Ａ君が９７番の座席に乗って頂上に向かい、途中で１番の座席とすれちがってから、次の２番の座席とすれちがうまでに４秒かかりました。
(１)
山のふもとから頂上までは何ｍですか。
(２)
１４番の座席がちょうど山のふもとに着きました。Ａ君が次にすれちがう座席は何番ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
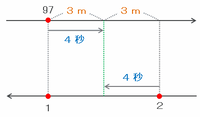
次の図のように、Ａ君の乗った９７番の座席と１番の座席がすれ違ってからの４秒間＝１５分の１分間で、９７番と２番の座席は向かい合わせで４５×１５分の１＝３ｍずつ進みます。
したがって、座席と座席の間は３×２＝６ｍ離れています。
※ 画像はすべて、クリックすると拡大します。
また、このリフトのコースは長方形なので、座席と座席の間の数は、座席の数と同じく１２３か所です。
※ 円や長方形など、１周できるコースの場合、木の数＝間の数。
つまり次の図のように、長方形の１周は６×１２３＝７３８ｍで、たて１辺と横１辺の長さの合計は７３８÷２＝３６９ｍです。
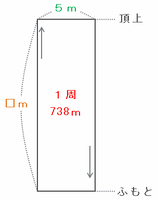
求めたいのはふもとから頂上までの距離(上の図の□ｍ)なので、答えは３６９－５＝３６４ｍになります。
(２)
１４番と１３番の座席は６ｍ離れているので、次の図のように１４番の座席がふもとに着いたとき、１３番の座席はふもとから６－５＝１ｍ進んだ地点にいます。
また、１３番の座席と１番の座席との間は１３－１＝１２か所、１番の座席と１２３番の座席との間が１か所、そして１２３番の座席と９７番の座席との間は１２３－９７＝２６か所あるので、１３番の座席と９７番の座席との間は１２＋１＋２６＝３９か所あります。
座席と座席との間はどこも６ｍなので、１３番の座席と９７番の座席は６×３９＝２３４ｍ離れており、１３番の座席はふもとから１ｍ進んだ地点にあるので、９７番の座席はふもとから２３４＋１＝２３５ｍ離れています。
そこで、次の図のように１４番の座席から２３５ｍ離れた地点について調べてみると、２３５÷６＝３９余り１なので、１４＋３９＝５３番の座席が、ふもとから６×３９＝２３４ｍ離れた地点にいることが分かります。
※ 余りの１は、９７番と５３番の座席が１ｍ離れていることを表す。
ただし、上の図を見れば分かるように、９７番と５３番の座席はすでにすれ違ってしまったので、次に９７番の座席がすれ違うのは、５３＋１＝５４番の座席です。
PR
