針金を折り曲げて、たてと横の長さの比が１：５の長方形Ａを作りました。次に、同じ長さの針金でたてと横の長さの比が４：５の長方形Ｂを作ると、Ｂの面積はＡの面積の何倍ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
とりあえず問題文の通りに、たてと横の長さの比が１：５と４：５になる長方形を次の図のようにかいてみると、同じ針金を使ったはずなのに、周りの長さは明らかにＢの方がＡより長くなってしまいます。
※ 画像はすべて、クリックすると拡大します。
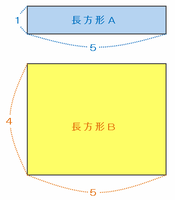
同じ針金で長方形を２つ作ったのだから、その２つの長方形の周りの長さはもちろん、たてと横の長さの和だって等しいはずです。
そこで次の図のように、２つの長方形のたてと横の長さの和を、１＋５＝６と４＋５＝９の最小公倍数である１８にそろえてみると、
・長方形Ａのたてと横の長さの比は３：１５
・長方形Ｂのたてと横の長さの比は８：１０
と表せることが分かります。
つまり、この２つの長方形を図に表すと次のようになるので、長方形Ａの面積は３×１５＝４５、そしてＢの面積は８×１０＝８０となります。
したがって、Ｂの面積はＡの８０÷４５＝
９分の１６倍です。
PR
