えんぴつ３本とマーカー２本は同じ値段です。はさみ２個とえんぴつ９本は同じ値段です。ノート２冊とえんぴつ７本は同じ値段です。ホチキス３個とはさみ５個は同じ値段です。消しゴム２１個とホチキス５個は同じ値段です。消しゴム１個とえんぴつ１本の値段の差は６６円です。えんぴつ１本は( )円、この６種類の文房具を１つずつ買うと、合計は( )円です。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
「比の内項と外項の積は等しい」ことを利用して、まずは次のように３組の比を求めてみます。
・えんぴつ×３＝マーカー×２なので、えんぴつ：マーカー＝２：３
・はさみ×２＝えんぴつ×９なので、はさみ：えんぴつ＝９：２
・ノート×２＝えんぴつ×７なので、ノート：えんぴつ＝７：２
これらの３つの比は、次の図のようにどれもえんぴつの値段を表す比が「２」でそろっているので、えんぴつ：マーカー：はさみ：ノート＝２：３：９：７となることが分かります。
※ 画像はすべて、クリックすると拡大します。
また、ホチキス３個とはさみ５個が同じ値段なので、ホチキスとはさみの値段の比は５：３となるのですが、さっき求めた比だとはさみの値段は「９」なので、次の図のように５：３を３倍して比をそろえてみます。
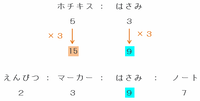
すると上の図のように、はさみの値段の比が９のとき、ホチキスの値段の比は１５と表せることが分かるので、えんぴつ：マーカー：はさみ：ノート：ホチキス＝２：３：９：７：１５となります。
消しゴム２１個とホチキス５個は同じ値段なので、消しゴムとホチキスの値段の比は５：２１となるのですが、さっきそろえた比だとホチキスの値段は「１５」なので、次の図のようにホチキスの値段の比が２１と１５の最小公倍数である１０５になるようにそろえてみます。
上の図から、６種類の文房具の値段の比は、えんぴつ：マーカー：はさみ：ノート：ホチキス：消しゴム＝１４：２１：６３：４９：１０５：２５となることが分かりました。
えんぴつと消しゴムの比の差は２５－１４＝１１なので、それが値段の差である６６円にあたります。
つまり、比の１は６６÷１１＝６円なので、えんぴつ１本の値段は６×１４＝８４円です。
また、６種類の文房具の値段の比を足すと１４＋２１＋６３＋４９＋１０５＋２５＝２７７となるので、６種類の文房具を１つずつ買ったときの値段の合計は６×２７７＝１６６２円になります。
PR
