重さのちがう３種類のコインＡ、Ｂ、Ｃがあります。これらをてんびんにのせると、Ｂ１枚がＣ３枚とつりあい、Ａ１枚とＣ１枚がＢ２枚とつりあいます。
※ 画像はすべて、クリックすると拡大します。
(１)
３種類のコインＡ、Ｂ、Ｃの重さの比をもっとも簡単な整数の比で表しなさい。
(２)
箱アにはＡ、箱イにはＢ、箱ウにはＣがそれぞれ何枚か入っています。ア、イ、ウに入っているコインの枚数の比は２：３：４です。ただし、箱の重さは考えません。
①
てんびんの片方にイを４箱置きました。てんびんをつりあわせるには、もう片方にアとウをそれぞれ何箱置けばよいですか。ただし、アとウは必ず１箱は置きます。
②
イ１箱とＢ２枚がア１箱とつりあいました。アには何枚のコインが入っていますか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
Ｂ１枚とＣ３枚の重さが同じということは、Ｂ１枚の重さはＣ１枚の３倍になるので、Ｂ１枚とＣ１枚の重さの比はＢ：Ｃ＝③：①と表せます。
このとき、次の図のようにてんびんの右側にあるＢ２枚をＣ６枚に変えてもつりあったままなので、「Ａ１枚とＣ１枚の重さの合計＝Ｃ６枚の重さ」であることが分かります。
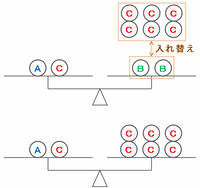
※ 画像はすべて、クリックすると拡大します。
ついでに左右の皿からＣを１枚ずつ取り除くと、次の図のようにＡ１枚とＣ５枚の重さが等しいことが分かるので、Ａ１枚とＣ１枚の重さの比はＡ：Ｃ＝⑤：①と表せます。
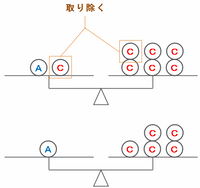
つまりＡ：Ｃ＝⑤：①、Ｂ：Ｃ＝③：①なので、Ａ：Ｂ：Ｃ＝⑤：③：①になります。
(２)の①
さっき求めたコイン１枚あたりの重さの比であるＡ：Ｂ：Ｃ＝⑤：③：①を使って、３つの箱それぞれの重さを比で表してみます。
・箱アの重さ→Ａが２枚入っているとすると、⑤×２＝[１０]
・箱イの重さ→Ｂが３枚入っているとすると、③×３＝[９]
・箱ウの重さ→Ｃが４枚入っているとすると、①×４＝[４]
このとき、次の図の左側には箱イが４つあるので、その重さの合計は[９]×４＝[３６]と表せます。
したがって、右側の皿にも箱アとウを組み合わせて[３６]の重さをのせてあげればつりあいます。
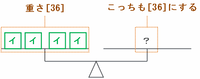
箱アの重さは１つあたり[１０]、箱ウの重さは１つあたり[４]、そしてどちらも必ず１箱以上は使うので、とりあえず箱アを１つ使った場合から考えてみると・・・
【箱アを１つ使った場合】
残りの重さは[３６]－[１０]＝[２６]となり、箱ウ１つの重さである[４]で割り切れないのでダメです。
【箱アを２つ使った場合】
箱ア２つ分の重さは[１０]×２＝[２０]、残りの重さは[３６]－[２０]＝[１６]なので、箱ウを[１６]÷[４]＝４つ置けばＯＫです。
以上から、右側の皿に箱アを２箱、箱ウを４箱置けばてんびんはつりあいます。
(２)の②
次の図のように、てんびんの右側には箱アが１つのっているので、その重さは[１０]と表せます。
このとき、左側の皿の重さの合計も[１０]、そして箱イ１つの重さは[９]なので、 [１０]－[９]＝[１]がＢ２枚分の重さにあたります。
[１]がＢ２枚分の重さなら、箱ア１つ分の重さである[１０]はＢ２０枚分の重さになります。
コイン１枚の重さの比はＡ：Ｂ＝⑤：③なので、Ｂ２０枚分の重さは③×２０枚＝６０になります。
つまり箱アに入っているＡの枚数を□枚とおくと、次の図のように⑤×□枚＝６０と表せるので、箱アの中にはＡが６０÷⑤＝１２枚入っています。
PR
