ある駅の通路には、一直線に、長さが６０ｍの動く歩道が２つあります。１つ目の動く歩道の始まりと終わりの地点をそれぞれＡ、Ｂとし、２つ目の動く歩道の始まりと終わりの地点をそれぞれＣ、Ｄとします。お父さんと明子さんはＡ地点からＤ地点に向かって同時にスタートしました。お父さんは動く歩道に乗り、明子さんは動く歩道にそって歩きました。お父さんは、１つ目の動く歩道の上では止まったまま乗っていたので、明子さんがＢ地点に来たとき、お父さんは明子さんより１５ｍ後ろにいました。その後、お父さんがＢ地点から歩き始めてＣ地点に来たとき、明子さんはお父さんより１７ｍ先にいました。そして、お父さんは、２つ目の動く歩道の上でもそのままの速さで歩いていたので、お父さんがＤ地点に着いたとき、明子さんはお父さんより１３ｍ後ろにいました。
※ 画像はクリックすると拡大します。
(１) 次の速さの比を、もっとも簡単な整数の比で表しなさい。
① 明子さんの歩く速さと、動く歩道の動く速さ
② 明子さんの歩く速さと、お父さんの歩く速さ
(２) ＢとＣの間の距離を求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)の①
ＡＢ間はお父さんが歩道の上で歩かずに止まっているので、そのときの速さの比を求めれば明子さんと動く歩道の速さの比が求められます。
明子さんが６０ｍ歩いてＢ地点に着いたとき、お父さんは次の図のようにＢより１５ｍ後ろの地点にいたので、明子さんが６０ｍ進むのにかかる時間で、動く歩道は６０－１５＝４５ｍ進みます。
※ 画像はすべて、クリックすると拡大します。
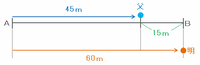
つまり、同じ時間に進む距離の比は明子：歩道＝６０ｍ：４５ｍ＝４：３なので、速さの比もそれと同じく４：３になります。
※ 速さの比＝同じ時間に進む距離の比
(１)の②
お父さんがＣ地点に到着したとき、明子さんはそれよりも１７ｍ先にいましたが、そこからはお父さんが動く歩道の上を歩いて進んでスピードアップして途中で追い越しました。
その結果、お父さんがＤ地点に着いたとき、明子さんは次の図のようにＤよりも１３ｍ後ろの地点にいました。
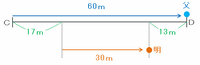
つまり、お父さんが動く歩道と自分の足のダブルパワーでＣＤ間の６０ｍを進む間に、明子さんは６０－(１７＋１３)＝３０ｍ進むので、「歩く明子さん」と「動く歩道＋歩くお父さん」の速さの比は３０ｍ：６０ｍ＝１：２になります。
さっきの問題で「歩く明子さん」と「動く歩道」の速さの比は４：３であることが分かったので、「歩く明子さん」と「動く歩道＋歩くお父さん」の速さの比も合わせて連比を求めてみると次の図のようになります。
上の図のように、「歩く明子さん」の速さの比を４とすると、「動く歩道」の速さの比は３、そして「動く歩道＋歩くお父さん」の速さの比は８と表せます。
つまり、「歩くお父さん」の速さの比は８－３＝５となるので、明子さんとお父さんの速さの比は４：５になります。
(２)
明子さんがＢ地点に着いたとき、お父さんはその１５ｍ後ろにいて、自分では歩かずに動く歩道の速さで進んでいます。
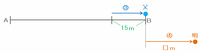
「歩く明子さん」と「動く歩道」の速さの比は４：３なので、次の図でお父さんが残りの１５ｍを進む間に明子さんが進む距離を□ｍとおくと、４：３＝□ｍ：１５ｍという比例式ができます。
４×１５÷３＝２０ｍなので、父がＢ地点に着いたとき、明子さんは次の図のようにそれよりも２０ｍ先の地点にいます。
その後、お父さんはＢＣ間を自分の足で歩き、Ｃ地点に着いたときには明子さんはそれよりも１７ｍ先の地点にいました。
「歩く明子さん」と「歩くお父さん」の速さの比は４：５なので、次の図のようにお父さんが歩いたＢＣ間の距離を⑤とおくと、そこから明子さんがいる地点までの距離は１７ｍなので、Ｂ地点から明子さんがいる地点までの距離は「⑤＋１７ｍ」と表せます。
また、お父さんがＢ地点にいたときに２０ｍリードしていた明子さんは、そこから④の距離だけ進んだので、Ｂ地点から明子さんがいる地点までの距離は「２０ｍ＋④」とも表せます。
「⑤＋１７ｍ」と「２０ｍ＋④」を次の図のような２本の線分図に書きかえて並べてみると、比の⑤－④＝①が２０－１７＝３ｍにあたることが分かります。
※ お父さんは比の⑤、明子さんは比の④だけ歩いたら、２人の距離の差が２０－１７＝３ｍ縮まったので、比の⑤－④＝①がその３ｍにあたる。
ＢＣ間の距離は比の⑤なので、答えは３×５＝１５ｍになります。
PR
