２００個の玉とＡ、Ｂ、Ｃ３つの空の袋があります。これから次の①～④の操作を順番に行います。
① Ａ、Ｂ、Ｃの３つの袋に、空の袋ができないように玉を入れる。ただし、玉は２００個全部を袋に入れなくてもよい。
② Ａの袋からいくつか玉を取り出し、Ｂの袋へ入れる。
③ Ｂの袋から、Ａの袋からもらった玉の２倍の数の玉を取り出し、Ｃの袋へ入れる。
④ Ｃの袋から、Ｂの袋からもらった玉の２倍の数の玉を取り出し、Ａの袋へ入れる。
①～④の操作を１度だけ行うとき、次の各問いに答えなさい。
(１)
①の操作でＡ、Ｂ、Ｃの３つの袋にそれぞれ同じ数の玉を入れました。④の操作を終えたとき、中に入っている玉が一番多い袋と一番少ない袋の玉の個数の差がもっとも大きくなる場合、その差は何個ですか。
(２)
④の操作を終えたとき、３つの袋に入っている玉の個数がすべて同じになりました。①の操作でＢの袋に入れられる玉の個数はもっとも多くて何個ですか。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
(１)
最初に３つの袋へなるべく多くの玉を入れておけば、やり取りを終えた後の袋に入っている玉の数の差も大きくなるはずです。
また、２００÷３＝６６余り２なので、２００個の玉を３つの袋へ同じ数ずつ入れるときの最大値は、次の図のようにどの袋も６６個となる場合です。
※ 画像はすべて、クリックすると拡大します。
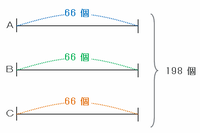
まずは次の図のように、Ａの袋からＢの袋へ渡した玉の数を①とおきます。
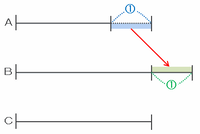
すると、次の図でＢからＣへ渡した玉の数は①×２＝②と表せます。また、この時点で
・Ａの袋→最初に比べてＢに渡した①の分だけ減った。
・Ｂの袋→Ａから①もらってＣへ②渡したので、最初に比べて②－①＝①減った。
となることから、下の図のＡとＢの袋に入っている玉の数は等しくなります。
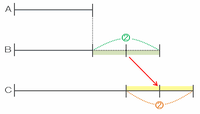
最後にＣからＡへ②×２＝④にあたる玉の数を渡すので、袋の中にある玉の数は次の図のようにＡが最も多く、Ｃが最も少なくなります。
３回のやり取りの後でＡとＣの袋の中に残った玉の数の差は次の図の赤い矢印部分なので、その数は比の①＋④＝⑤と表せます。
その個数をなるべく多くするためには、下の図の赤い矢印の幅をなるべく広く、そして紫色の矢印の幅をなるべくせまくしてやればＯＫです。
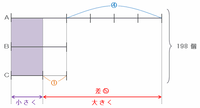
つまり次の図のように、紫色の部分を０個にすれば赤い矢印の幅が最も広くなり、そのときのＡの袋にある玉の個数は比の⑤、Ｂの袋にある玉の個数は比の①、そしてＣの袋には玉が１個も残っていない状態になります。
※ ＣからＡへ渡した玉の数である④が、その時点でＣの袋に入っていた玉の数の合計と等しかった。
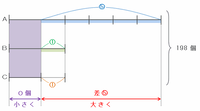
上の図の１９８個は、比の⑤＋①＝⑥にあたるので、比の①は１９８÷⑥＝３３個になります。
また、ＡとＣの袋の中にある玉の数の差は比の⑤にあたるので、答えは３３×⑤＝１６５個です。
(２)
次の図は、最後にＣがＡへ比の④にあたる数の玉を渡したときに３つの袋の玉の数がそろった状態を表しています。
図の青い部分は３つの袋の中に入っている比の④にあたる玉の数、そして紫色の部分は玉のやり取りとは無関係だった部分です。
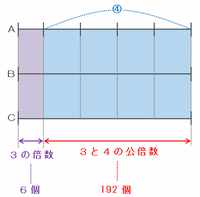
上の図の青い部分は、４等分できる線が全部で３本あるので、玉の数の合計は３と４の公倍数になります。
また、紫色の部分は同じ長さの線が３本あるので、玉の数の合計は３の倍数になります。
さっきの問題のときと同じように、図の赤い矢印の幅をなるべく広く、そして紫色の矢印の幅をなるべくせまくしてみると、
・赤い矢印…２００以下の１２の倍数の中で最も大きい１９２個を３袋に分けて６４個ずつ
・紫色の矢印…２００－１９２＝８個、８÷３＝２余り２なので３袋に２個ずつ
のように分けられます。
まずは次の図のように、最後にＣからＡへ渡した比の④にあたる６４個をＣへ返してあげると、Ａの袋の中には玉が２個だけ残ります。
ＢからＣへ渡した玉の個数は比の②にあたる３２個なので、それも次の図のようにＢへ返してあげます。
このとき、ＢとＣの袋の中にある玉の個数は等しくなります。
最初にＡからＢへ渡した玉の個数は比の①にあたる１６個なので、次の図のようにそれをＡの袋へ戻してあげます。
つまり、玉のやり取りをする前の３つの袋には次の図のように玉が入っていたことが分かるので、Ｂの袋に入っていた玉の数は２＋６４＋１６＝８２個になります。
【補足】
もし次の図のように、紫色の矢印の幅をなるべく広く、そして赤い矢印の幅をなるべくせまくしてみた場合、
・赤い矢印…３と４の最小公倍数である１２個を３袋に分けて４個ずつ
・紫色の矢印…２００－１２＝１８８個、１８８÷３＝６２余り２なので３袋に６２個ずつ
のように分けられるので、比の①は４÷④＝１個になります。
すると、やり取りをする前の３つの袋に入っている玉の数は次の図のようになるため、Ｂの袋には６２＋４＋１＝６７個の玉が入っています。
しかし、それだとさっき求めた８２個よりも少なくなってしまうので、この分け方ではダメなんだ、ということが分かります。
PR
