兄と弟がお金を出し合って６０００円のサッカーボールを１個買いました。兄は自分の所持金の２分の１を、弟は自分の所持金の３分の１をそれぞれ出し合ってその代金を支払いました。残った所持金を比べたところ、兄の金額は弟の金額の２倍でした。代金を支払う前の兄弟の所持金をそれぞれ求めなさい。
※ 続きを見る場合は、下の「解説はこちらから」をクリック！
まずは２人の残金の比を求めてみると、兄の残金は弟の残金の２倍なので、残金の比は兄：弟＝２：１になります。
次に２人の残金を割合で求めてみると、兄は最初の所持金の２分の１を使ったので残金も２分の１、そして弟は最初の所持金の３分の１を使ったので、残金は１－３分の１＝３分の２になります。
ここまで分かったことをもとにして、兄の最初の所持金を□円、弟の最初の所持金を△円とおいて線分図に表すと次のようになります。
※ 画像はクリックすると拡大します。
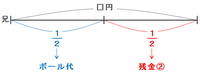
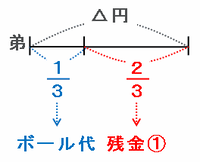
上の線分図を利用して兄と弟それぞれの最初の所持金の割合を求めてみると、次のようになります。
兄→最初の所持金(図の□円)の２分の１が残金の比である２にあたるので、最初の所持金は２÷２分の１＝４と表せます。
弟→最初の所持金(図の△円)の３分の２が残金の比である１にあたるので、最初の所持金は１÷３分の２＝１.５と表せます。
つまり、兄と弟の最初の所持金の比は、兄：弟＝４：１.５＝８：３になります。
次に兄と弟それぞれが出したボール代の割合を求めてみると・・・
兄→最初の所持金である８の２分の１を出したので、８×２分の１＝４と表せます。
弟→最初の所持金である３の３分の１を出したので、３×３分の１＝１と表せます。
となるので、ボールの代金である６０００円は比の４＋１＝５にあたります。
比の１は６０００÷５＝１２００円なので、兄の最初の所持金は１２００×８＝９６００円、そして弟の最初の所持金は１２００×３＝３６００円になります。
PR
